りんご2個を3回コピーしてみよう!
りんごが2個あったとします。
これを3回コピーすると、りんごは何個になりますか?
※ただし、もとのりんごの数は除きます。
つぎの図をみれば、合計6個になることがわかります。
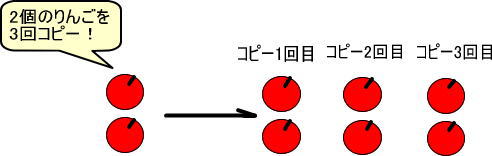
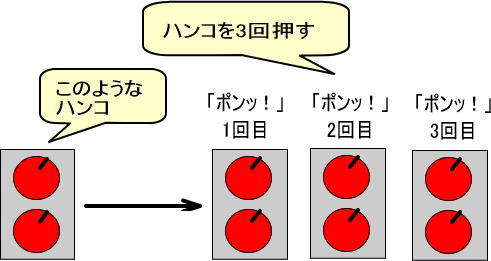
なお、「コピー」の考えかたが難しいのなら、つぎの図のような「ハンコ」を想像するといいでしょう。
このハンコを3回、「ポンッ!」と押すと、りんごは合計6個になるとわかります。
スポンサード リンク
かけ算の計算の際には「コピー」や「ハンコ」をイメージしよう!
(問)「3×4」を計算してみましょう。
「3×4」の「×4」は「4をかける」という意味ですが、「3」は「りんご3個」、「×4」は「4回コピーする」と考えます。
というわけで、「3×4」は、「りんご3個を4回コピーする」となるので、つぎの図のようになります。
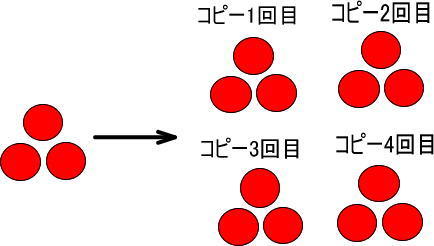
※「コピー」が難しいのなら、「×4」を「4回ハンコを『ポンッ!』と押す」と考えるといいでしょう。
3のハンコを4回、「ポンッ!」と押すので、つぎの図のようになります。
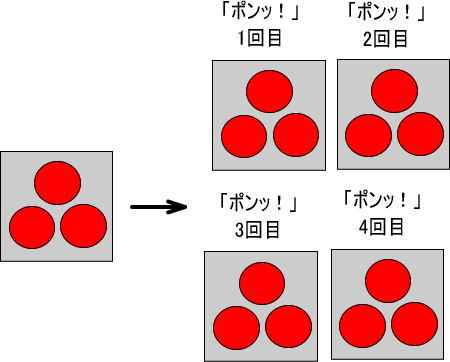
いずれの場合も、りんごを数えると、「12」だとわかります。
よって、「3×4=12」となります。
<まとめ>
「▲×●」を見れば、つぎのように考えるといいでしょう。
・「▲」は「りんご▲個」
・「×●」は「●回コピーする」「ハンコを●回、ポンッと押す」
スポンサード リンク
かけ算の練習をしよう!
(問)「5×2」を計算してみましょう。
「5」は「りんご5個」、「×2」は「2回コピーする」と考えると、「5×2」は「りんご5個を2回コピーする」となります。
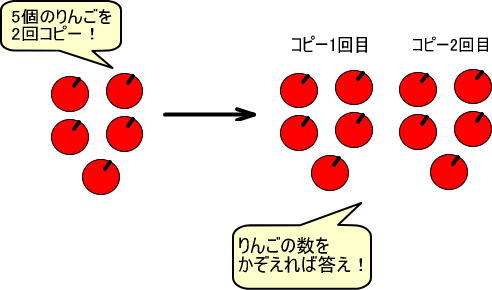
りんごの数をかぞえると、答えは「10」だとわかります。
【難問にチャレンジ!】「かけ算はコピー」とわかれば、かんたんな方程式なら解ける!
※ここからはすこし難しいので、読んでみて、すこしでもわからないと感じれば、いまは飛ばして構いません。あとでもう一度、勉強します。
(問)「〇×3」を計算すると9になりました。〇はいくつだと思いますか。
「×3」は「3回コピーする」なので、「〇×3」は、「〇を3回コピーする」という意味になります。
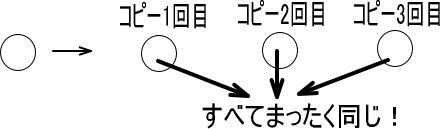
これを図で表すと、つぎのようになります。
※〇のハンコを3回、ポン、ポン、ポンと押したと考えても構いません。

〇はコピーしたものなので、それぞれ、まったく同じですよね。
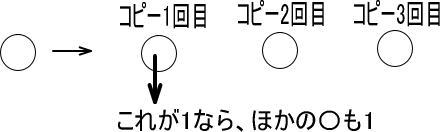
さて、ここで、〇の正体が「1」だったとします。
すると、ほかの〇もすべて「1」になりますよね。
1が3つあるので、数えると「3」になります。
ここで問題文をもう一度よく読んでみてください。
「〇×3を計算すると9だった」とあります。
もし〇が1ならば、「〇×3」を計算すると3になるので、〇は1ではありません。
では、〇の正体が「2」であれば、どうでしょうか。
ほかの〇もすべて「2」になります。
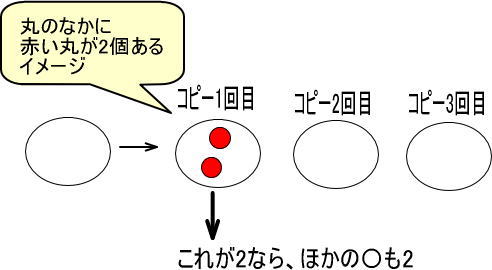
2が3つあるので、数えると「6」になります。
問題文に「〇×3を計算すると9だった」とあるので、〇は2でもありません。
では、〇の正体が「3」であれば、どうでしょうか。
ほかの〇もすべて「3」になります。
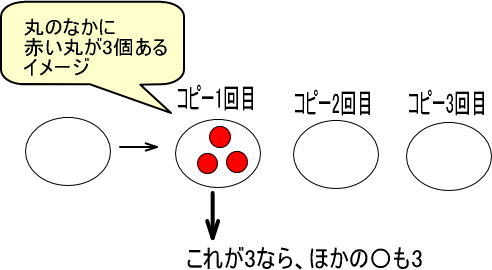
3が3つあるので、数えると「9」になります。
問題文に「〇×3を計算すると9」とあるので、〇は3であることとわかります。
答えは「〇=3」です。
さて、「〇×3を計算すると9」を式で表すと「〇×3=9」です。
これは方程式といわれるもので、中学一年生のときに勉強する内容です。
しかし、「コピー」や「ハンコ」をイメージできると、かんたんな方程式であれば解けてしまうのですね。
スポンサード リンク
【参考】コピーやハンコではなくても……。
「コピーやハンコをイメージしなくても、かけ算くらいわかるよ」
このように思うひともいるかもしれませんし、算数や数学が得意なひとは「まわりくどい」と感じるようです。
しかし、算数や数学が苦手ならば、この考えかたを知っておくと「将来」楽になります。
具体的には、中学のときに勉強する「文字式」のところで役立ちます。
算数や数学が得意なひとは、コピーやハンコをイメージしなくても、文字式をスッと理解できますが、苦手なひとにはなかなか理解できないものです。
そこで、ここで紹介した考えかたの登場です。
「かけ算はコピー」「かけ算はハンコ」と覚えていれば、理解しやすくなります。
その話はまた追々と。