かけ算とわり算の不思議な関係
このページの話はすこしややこしいので、まずは今までのレッスンをしっかり復習してください。
また、このページは気を抜かず、しっかり読んでください。
「わからない」と思えば、何度も読み返すことをお勧めします。
(1)まずは「かけ算」を図で表してみよう!
「3×2」を計算してみましょう。
「3」は「りんご3個」と考えるのでした。
今回はりんごを箱にいれます。

「×2」は「2回コピーする」という意味でした。
よって、「3×2」は「箱に入ったりんご3個を、2回コピーする」となります。
このとき、つぎのように図をすこし工夫します。
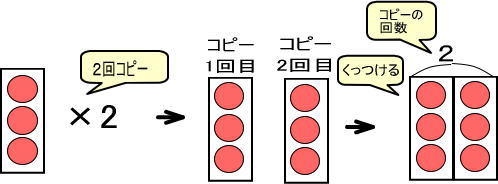
これを式で表すと「3×2=6」となります。
(2)「かけ算」の図を逆から見ると「わり算」に!
ここで上図を逆から見てみてください。
つぎのようにできます(これは上図の順番を逆にして、(a)と(b)の文字を書き加えただけです)。
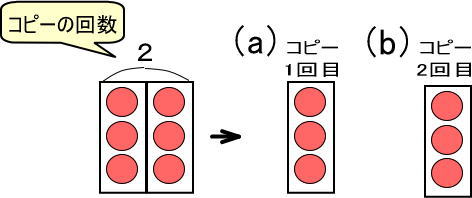
さて、ここで(a)と(b)に着目してください。
コピーしたわけなので、(a)も(b)もまったく同じものです。
すなわち、この図はつぎのように考えることもできます(2つに等しく分ければ、まったく同じ箱が2つできます。その2つの箱が(a)と(b))。
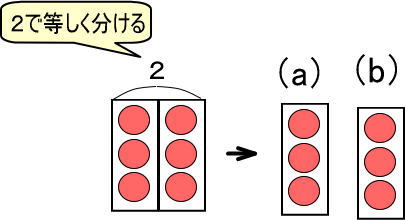
りんご6個を2つに等しく分けています。
式で表すと「6÷2」です。
これを図で表すと、つぎのようになります(これも「わり算」のところで、すでに学習しています)。
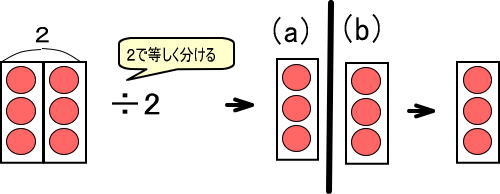
数えるとりんごは3個なので、式で表すと「6÷2=3」となります。
まとめ
まとめます。
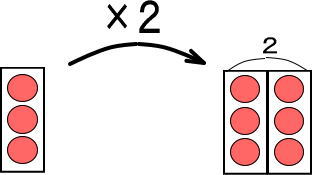
(1)「3×2=6」を図にすると、つぎのようになりました。

(2)(1)を逆から見ると、つぎの図になりました。式で表すと「6÷2=3」になりました。

要は「3×2=6」も「6÷2=3」も同じということですね。
ここからが本題!
(1)ですが、図はつぎのようになりました。

これを、かんたんにします。
(2)ですが、図はつぎのようになりました。
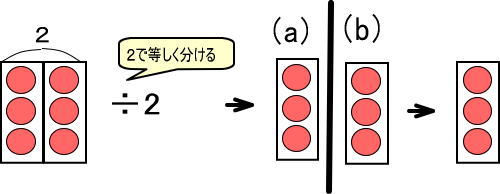
これを、かんたんにします。
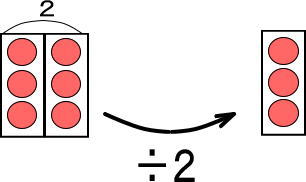
左右ひっくり返します。
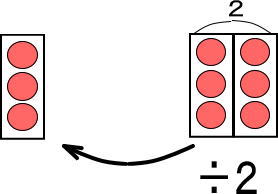
まとめると、つぎのようにできます。
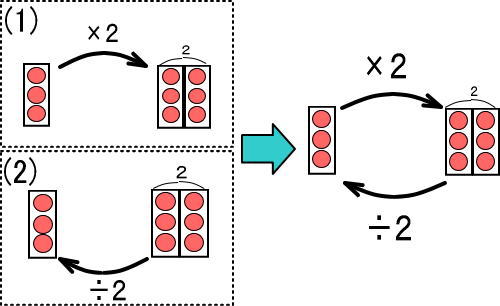
これを数字にすると、つぎのようになります。
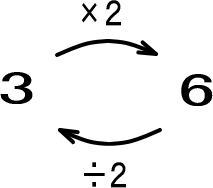
3に2をかければ6。
6からもとの3に戻したければ2で割ればいいとわかります。
かけ算とわり算には、このような関係があるわけですね。
非常にわかりにくいところなので、もう一例あげてみます。
スポンサード リンク
もう一例でかけ算とわり算の関係を理解しよう!
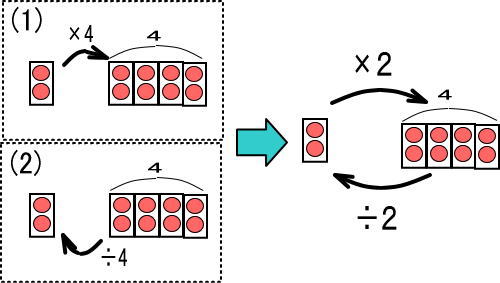
(1)「2×4」を図で表してみてください。
「×4」は「4回コピーする」なので、つぎのようになります。
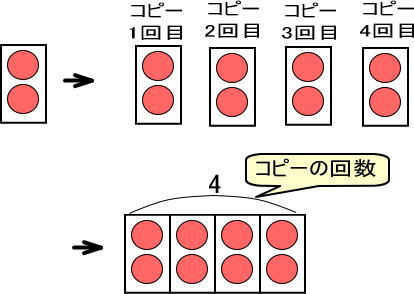
「2×4=8」です。
この図をかんたんにすると、つぎのようになります。
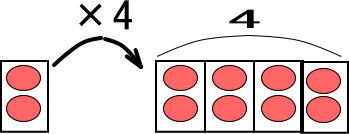
(2)(1)の図を逆から見てください。
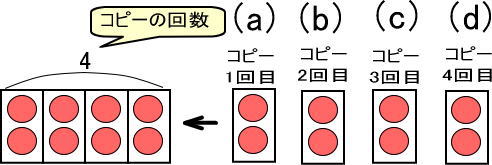
さて、ここで(a)〜(d)に着目してください。
コピーしたわけなので、(a)も(b)も(c)も(d)も、まったく同じものです。
すなわち、この図はつぎのように考えることもできます。
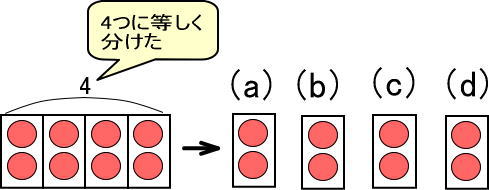
8個あるりんごを4つに等しく分けるわけなので、つぎのように表せます。
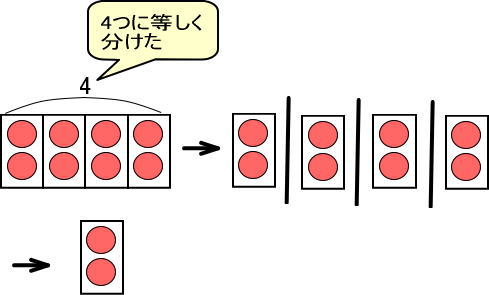
これを式で表すと「8÷4=2」となります。
この図をかんたんにして、左右ひっくり返すと、つぎのようになります。
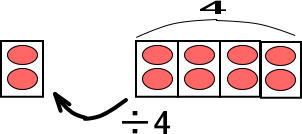
以上をまとめます。
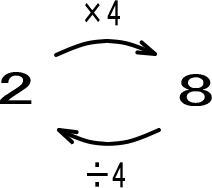
2に4をかければ8。
8からもとの2に戻したければ4で割ればいいとわかります。
やはり、かけ算とわり算は、このような関係があるわけです。