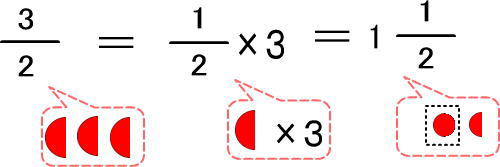「かけら」をイメージすれば分数はわかる！

「かけら」をイメージすれば分数はわかる！

「1÷2」を計算してみましょう。

「1」は「りんご1個」、「÷2」は「ナイフを使って等しく2つに分ける」という意味なので、「1÷2」は「りんご1個をナイフを使って等しく2つに分ける」となります。
要は、りんご1個を真っ二つに割るということなので、図で表すと、つぎのようになります。



さて、ここで質問です。
この「かけら」となったりんごは、数字でどのように表せばいいと思いますか。



「分数」を使います。
具体的にはつぎのように表します。



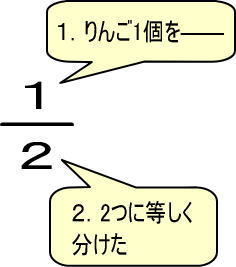
よって、「1÷2＝1／2」となります。

では、「3÷2」を計算してみましょう。

「3」は「りんご3個」、「÷2」は「ナイフを使って等しく2つに分ける」という意味なので、「3÷2」は「りんご3個をナイフを使って等しく2つに分ける」となります。
図で表すと、つぎのようになります。



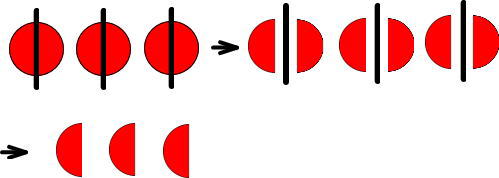
これらの「かけら」となったりんごは、どのように表せばいいと思いますか。
つぎのようになりますね。



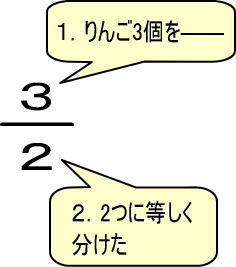
よって、「3÷2＝3／2」となります。

＜まとめ＞
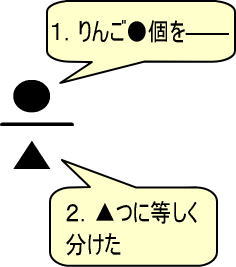
「●÷▲」はつぎのように表します。

・りんご●個
・▲で等しく分ける

分数の性質その1

先ほどの「3÷2」の図をもう一度みてください。



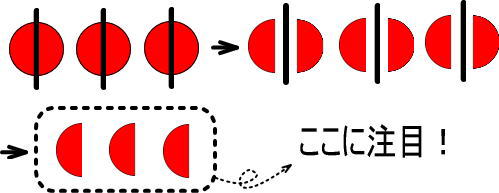
「ここに注目」にある、りんごのかけらは「3／2」と表せましたね。

さて、ここで、これらの3つのかけらのうち、1つのかけらに注目してください。
上図をよく見ると、りんご1個を2つに等しく分けたときのかけらだとわかります。
りんご1個を2つに等しく分けたわけなので、数字で表すと「1／2」です。



このかけらが3個あります。
この3個のかけらは、すべてまったく同じです。
「まったく同じものが3個」は、「3回コピーした」、すなわち「×3」と考えることもできるので（すでに学習しました）、つぎのようにできます。



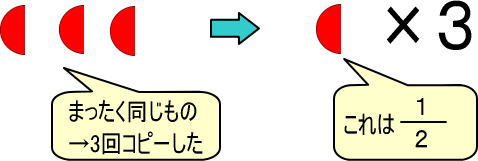
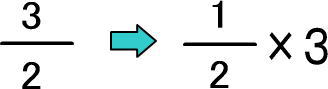
よって、つぎのようにできます。

分数の性質その2

ふたたび、先ほどの「3÷2」の図をみてください。



「ここに注目」にある、りんごのかけらは「3／2」と表せました。

さて、ここで、これらの3つのかけらのうち、2つのかけらに注目してください。

1つのかけらは、りんご1個を2つに等しく分けたときのかけらでした。
よって、かけら2つをくっつけると、「1個のりんご」になるとわかります。



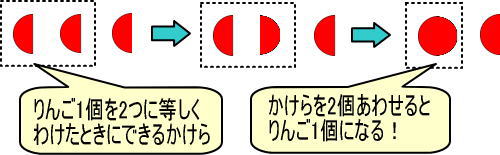
これを数字で表すと、つぎのようになります。

分数の性質〜まとめ〜

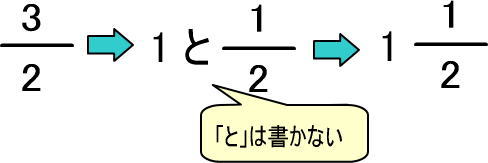
まとめると、「3／2」はつぎのように形を変えることができます。