中学受験では、かけ算の方程式は「面積図」を使って解く
※中学受験では面積図を使う機会がありますが、中学生以降は一切使いません。中学受験を考えていないのなら、読み流す程度で構いません。
まずは、復習です。
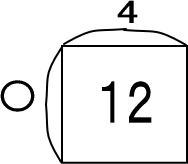
〇はいくつなのか求めるとき、「〇=12÷4」で計算しましたね。
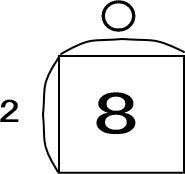
こちらも〇はいくつなのか求めるとき、「〇=8÷2」で計算しました。
「面積」を「1つの辺の長さ」で割れば、「もう一つの辺の長さ」が計算できるのでした(これも、すでに前のレッスンで学習しました)。
復習はここまでです。
では、「9÷〇=3」を解いてみましょう。
解きかたは、前のレッスンと同じです。
1.四角形の図を描いて、2.そこに数字をあてはめる、という2ステップで解きます。
1.まずは四角形を書きます。
2.上記1に「9÷〇=3」の数字をあてはめるのですが…。すぐにわかるでしょうか。
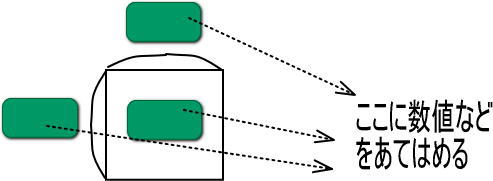
つぎの2つをよく見比べてみてください。
・「面積」を「1つの辺の長さ」で割れば、「もう一つの辺の長さ」が計算できる
・「9÷〇=3」
すると、つぎのように考えられるとわかるはずです。
・9:面積
・〇:1つの辺の長さ
・3:もう1つの辺の長さ
よって、図はつぎのようになります。
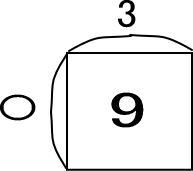
この図は見たことがありますね。
「〇=9÷3=3」となります。
わり算の方程式はこのようにして解けばいいのですが、わかったような、わからないような…という気持ちだと思うので、もう一問解いてみましょう。
スポンサード リンク
かけ算を四角形に当てはめたのが面積図
「12÷〇=4」を解いてみましょう。
つぎの2つをよく見比べてみてください。
・「面積」を「1つの辺の長さ」で割れば、「もう一つの辺の長さ」が計算できる
・「12÷〇=4」
つまり、この式は、つぎのようにも考えられるとわかるはずです。
・12:面積
・〇:1つの辺の長さ
・4:もう1つの辺の長さ
よって、図はつぎのようになります。
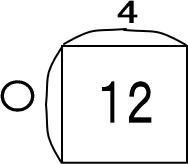
「〇=12÷4=3」となります。
このように、つぎのようなわり算の方程式がでてくれば面積図を描くといいでしょう。
(例1)12÷x=3
(例2)10=20÷x
(例3)x÷8=2
スポンサード リンク
面積図のまとめ
※●、▲、■と、数字を使っていないので難しく感じるかもしれません。「なんかややこしい」と思えば、ここはわからなくても構いません。
一つの辺の長さが●、もう一つの辺の長さが●、面積が■の四角形があったとします。
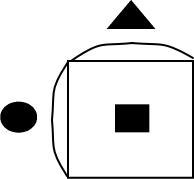
一辺の長さと、もう一辺の長さをかけると面積になりました。
・●×▲=■
面積は、一辺の長さと、もう一辺の長さをかけると計算できます。
・■=●×▲
「面積」を「1つの辺の長さ」で割れば、「もう一つの辺の長さ」が計算できます。
・■÷●=▲
・■÷▲=●
「一つの辺の長さ」を計算するには、「面積」を「もう1つの辺の長さ」で割ります。
・▲=■÷●
・●=■÷▲
すなわち、つぎの式を図で表すと――。
・●×▲=■
・■=●×▲
・■÷●=▲
・■÷▲=●
・▲=■÷●
・●=■÷▲
すべて、つぎの図になるのですね。

ほとんどのひとが「よくわからない…」と思ったことでしょう。
よくわからないと思えば、実際につぎの式の●、▲、■を、四角形に当てはめてみてください。
具体的には、つぎの式のそれぞれの●、▲、■を1つずつ――。
・●×▲=■
・■=●×▲
・■÷●=▲
・■÷▲=●
・▲=■÷●
・●=■÷▲
つぎのようにあてはめてみてください。

すべて、つぎの図になるとわかるはずです。
