中学受験では、たし算、ひき算の方程式は「線分図」を使って解く
※中学受験では線分図を使う機会がありますが、中学生以降は一切使いません。とはいえ、文章題などで似たような図を使うことがあるので、中学受験を考えていなくても理解しておくことをお勧めします。
まずは、復習です。
「2+3=5」を数直線で表してください。
この式を「すごろく」にすると、つぎのようになりますよね。
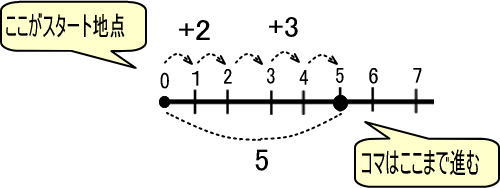
「+2」「+3」でゴールが「5」
これを数直線にすると、つぎのようになります。
ここまではすでに学習したのでわかると思います。
さて、ここで数直線を、つぎのようにかんたんにしてみます。
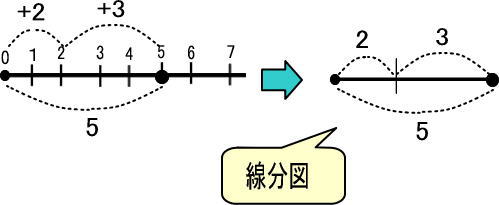
上図の右のようなものを「線分図」といいます(いまのところは、このように理解してください)。
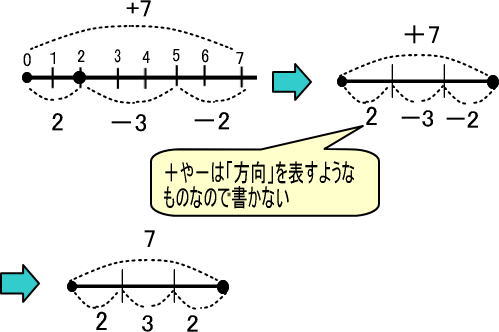
※なお、「+」は「右に」、「−」は「左に」という意味で「方向」を表すようなものなので、+や−は線分図では書きません。注意してください。
というわけで、「2+3=5」の線分図は上図の右になるわけですね。
では、「6−3=3」を線分図で表してみましょう。
この式を「すごろく」にすると、つぎのようになります。
「+6」「−3」で、ゴールが「3」
これを数直線で表すと、つぎのようになります。
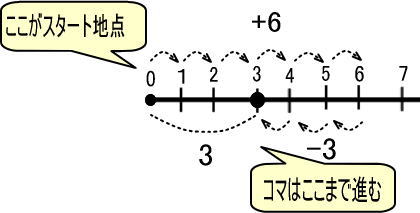
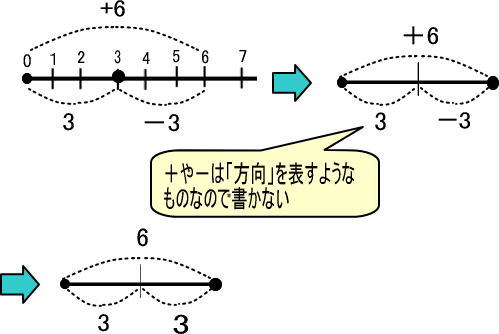
この図をかんたんにしますが、この際に注意することがありました。
「+」は「右に」、「−」は「左に」という意味で「方向」を表すようなものなので、線分図では+や−は書かないのでした。
よって、つぎのようになります。
スポンサード リンク
線分図を描く練習をしよう!
「7−2−3=2」を線分図で表してみましょう。
この式を「すごろく」にすると、つぎのようになります。
「+7」「−3」「−2」で、ゴールが「2」
これを数直線で表すと、つぎのようになります。
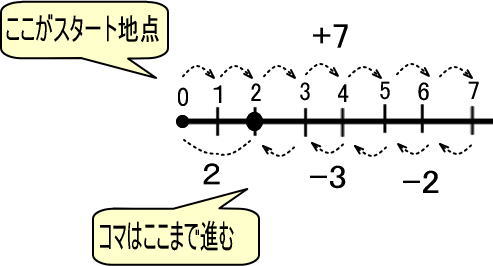
この図をかんたんにすれば、つぎのようになります。
では、最後に「●−▲=■」を線分図で表してみましょう。
※いまの時点では難しいと感じるかもしれませんが、今までの話がわかっていればなんとかできるはずです。
※細かいことをいうひとのために、条件を書くと「●>▲>0」です。
この式を「すごろく」にすると、つぎのようになります。
「+●」「−▲」で、ゴールが「■」
数直線で表すと、つぎのようになります。
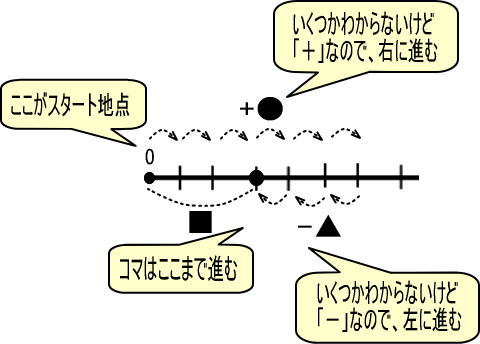
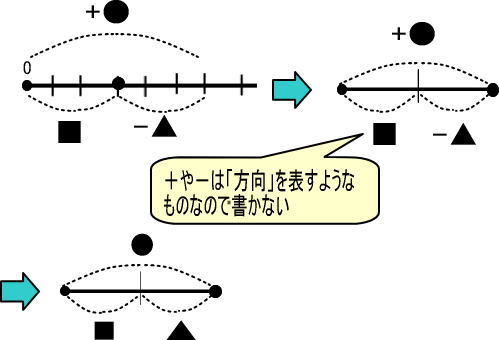
この図をかんたんにすれば、つぎのようになります。
なお、線分図では+や−は書かないでくださいね。
スポンサード リンク
線分図を使って、方程式を解いてみよう!
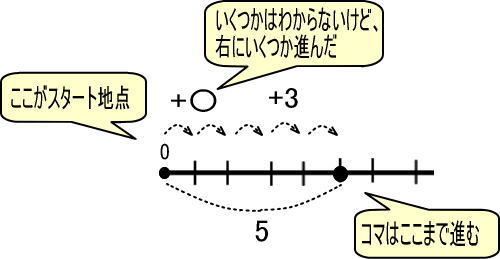
「〇+3=5」の〇を求めてみましょう。
この式を「すごろく」にすると、つぎのようになります。
「+〇」「+3」で、ゴールが「5」
これを数直線で表すと、つぎのようになります。
この図をかんたんにすれば、つぎのようになります。
なお、線分図では+や−は書かないでくださいね。
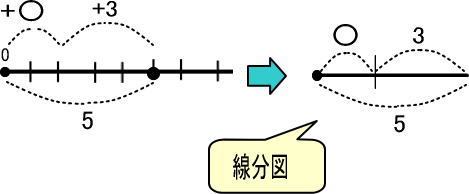
〇は「5」から「3」を引けばわかりますね。
よって、「〇=5−3=2」です。
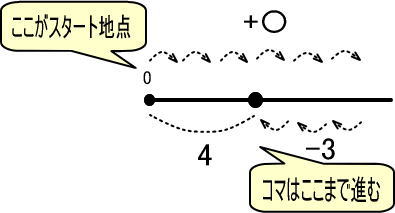
つぎに「〇‐3=4」の〇を求めてみましょう。
この式を「すごろく」にすると、つぎのようになります。
「+〇」「−3」で、ゴールが「4」
数直線で表すと、つぎのようになります。
この図をかんたんにすれば、つぎのようになります。
なお、線分図では+や−は書かないでくださいね。
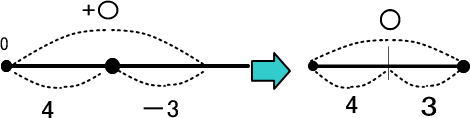
〇は「4 」と「3」を足せばいいとわかりますね。
よって、「〇=4+3=7」です。
先に計算できるところは、計算しておこう!
「12−〇+2=6」の〇を求めてみましょう。
この式を「すごろく」にすると、つぎのようになります。
「+12」「−〇」「+2」で、ゴールが「6」
数直線で表すと、つぎのようになります。
※コマの進めかたがすこしややこしいので、今回は「(1)+12」「(2)−〇」「(3)+2」と番号をつけました。
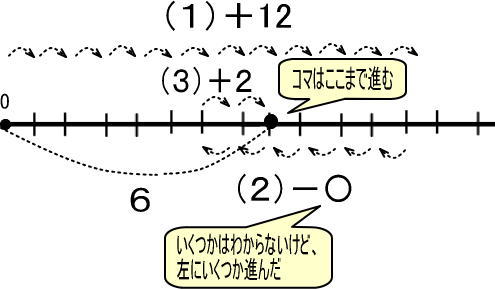
この図をかんたんにして線分図にしたいところですが…。
ややこしくて線分図にしたくないと思います(できなくはないのですが…)。
では、どうすればいいのでしょうか。
問をもう一度みてみてください。
つぎのように、まだ計算できるとわかります。
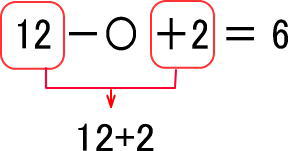
よって、問は「14−〇=6」となります。
この式を「すごろく」にすると、つぎのようになります。
「+14」「−〇」で、ゴールが「6」
これを数直線で表すと、つぎのようになります。
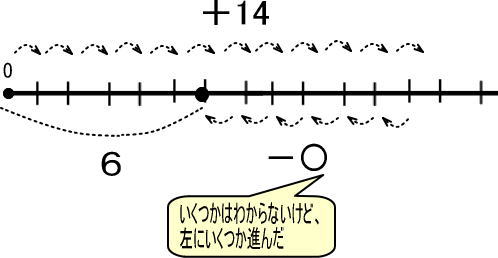
この図をかんたんにすれば、つぎのようになります。
なお、線分図では+や−は書かないでくださいね。
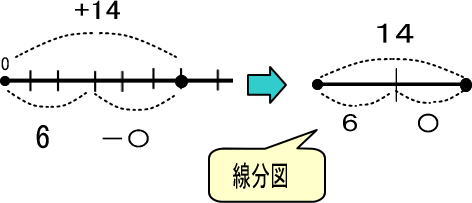
〇は「14」から「6」を引けばわかりますね。
よって、「〇=14−6=8」です。
このように、問の式に計算できるところがあれば最初に計算してしまいましょう。