方程式は線分図と面積図で解こう!
※中学受験では方程式を線分図と面積図で解きますが、中学生以降は文字式を使って解きます。中学受験をしないなら、読み流す程度で構いません。
「2×x−3=3」のxを求めてみましょう。
このような「=」で結ばれた式を方程式というのでした。
方程式は、つぎの2ステップで解きます。
(ステップ1) 線分図を使う
(ステップ2) 面積図を使う
まずは、ステップ1の線分図を使います。
この際、「2×x」の部分を指で隠すといいでしょう。
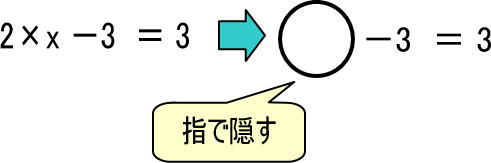
この式を「すごろく」にすると、つぎのようになります。
「+〇」「−3」とコマを進めるとゴールが「3」
これを数直線で表すと、つぎのようになります。
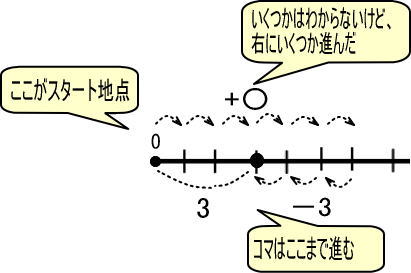
この図をかんたんにします。
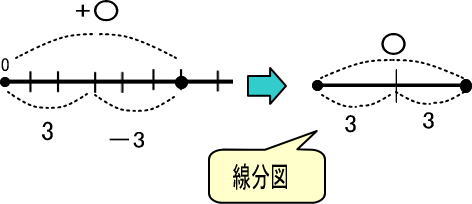
よって、「〇=3+3=6」になります。
さて、もう一度、いままでの話を読み返してみてください。
すると「〇=2×x」だと思い出すはずです。
つまり、「2×x=6」となりますね。
ここまでできれば、つぎはステップ2の面積図を使います。
「2×x=6」の2、x、6をつぎの四角形にあてはめてみてください。
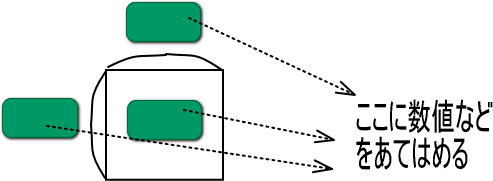
しっかり復習できていれば、つぎのようにできるとわかります。
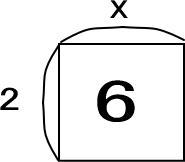
しっかり復習できていれば、「x=6÷2=3」だとわかります。
スポンサード リンク
方程式は2ステップで解ける!
方程式は2ステップで解きましたが、詳細に手順を書くとつぎのようになります。
(ステップ1) 「●+▲×x−★=■」のような、「たし算」「ひき算」がある式を、線分図を使って「●×x=■」のような形にします。この際、「▲×x」とxがある部分を指で隠すとみやすくなります。
※先ほどは「2×x−3=3」を、線分図を使って「2×x=6」の形にしました。また「2×x」の部分を指で隠しました。
(ステップ2) 「●×x=■」のような式に、面積図を使って、xがいくつかのかを求めます。
※先ほどは、「2×x=6」に面積図を使って、x=3と求めました。
何事でも最初はややこしく感じるものです。
いくつか問を解いて慣れましょう。
(問1)「3×x+3=9」のxを求めてみましょう。
まずはステップ1の線分図を書きます。
この際、「3×x」の部分を指で隠せばいいのでした。
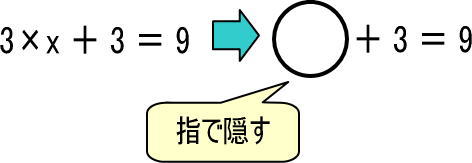
この式を「すごろく」にすると、つぎのようになります。
「+〇」「+3」とコマを進めるとゴールが「9」
これを数直線で表すと、つぎのようになります。
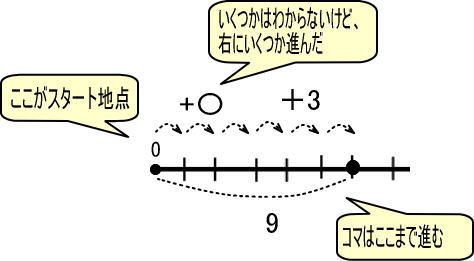
この図をかんたんにします。
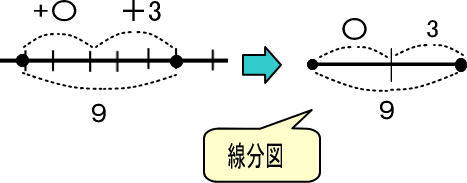
線分図を見れば「〇=9−3=6」だとわかります。
さて、もう一度、いままでの話を読み返してみてください。
すると「〇=3×x」だと思い出すはずです。
つまり、「3×x=6」ですね。
ここまでできれば、つぎはステップ2の面積図を使います。
「3×x=6」の3、x、6をつぎの四角形にあてはめてみてください。

しっかり復習できていれば、つぎのようにできるとわかります。
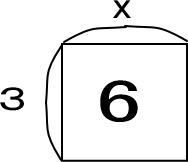
「x=6÷3=2」だとわかります。
(問2)「12−4×x+2=6」のxを求めてみましょう。
まずはステップ1の線分図を書きます。
この際、「4×x」の部分を指で隠せばいいのでした。
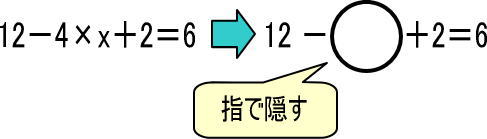
よく見ると、計算できるところがあります。
計算してしまいましょう。
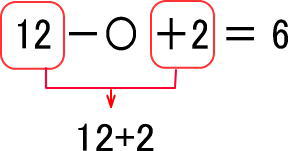
よって、問は「14−〇=6」となります。
この式を「すごろく」にすると、つぎのようになります。
「+14」「−〇」とコマを進めるとゴールが「6」
これを数直線で表すと、つぎのようになります。
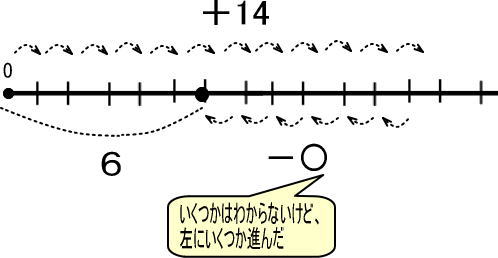
この図をかんたんにします。
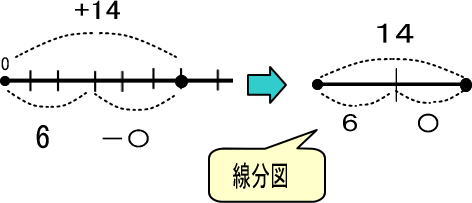
線分図を見れば「〇=14−6=8」だとわかります。
さて、もう一度、いままでの話を読み返してみてください。
すると「〇=4×x」だと思い出すはずです。
つまり、「4×x=8」ですね。
ここまでできれば、つぎは面積図を使います。
「4×x=8」の4、x、8をつぎの四角形にあてはめてみてください。

しっかり復習できていれば、つぎのようにできるとわかります。
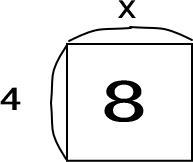
「x=8÷4=2」だとわかります。
スポンサード リンク
線分図と面積図はいずれ卒業!
方程式の解きかたです。
(中学受験)線分図と面積図を使って解く
(中学生以降)文字を使った式を変形して解く
「線分図と面積図を使いこなせるようになれば、文字を使った式の変形もかんたんに理解できるようになる!」と主張している先生もいますし、そういう理解のしかたが向く子どももいます。
しかし、線文図や面積図では方程式を解けるのに、文字を使った式の変形が理解できない子どももいます。
線分図や面積図を使って方程式を解く方法は中学受験特有のものですし、文字を使った式の変形さえ理解できれば中学生以降、困ることもありませんので、中学受験をしないのならば線分図や面積図は読み流すくらいでOKと書いた次第です。
※わたし自身、中学受験を経験していないので、方程式を線分図と面積図を解く方法は大人になってから知りました。
ただ、線分図については文章題をはじめ、さまざまなところで使う機会があるので、しっかり描けるようになっておくほうがいいです。