わりきれない場合は「あまり」で表す
「5÷2」を計算してみましょう。
「5」は「りんご5個」、「÷2」は「ナイフを使って2つに等しく分ける」という意味でした。
しかし、2つに等しく分けることができません。
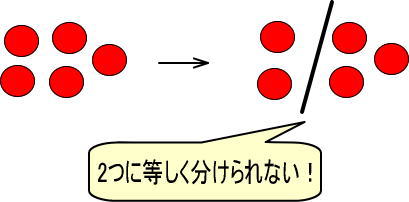
このような場合は、分数や少数で表すのですが、それ以外にも「あまり」を使って表すこともできます。
あまりとは一体どういうものでしょうか。
また、どのように表すのでしょうか。
スポンサード リンク
あまりを式で表してみよう!
まずは復習です。
(例1)4÷2
「÷2」は「ナイフで2つに等しく分ける」という意味でした。
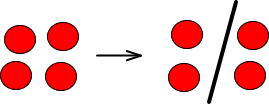
等しく2個ずつに分けられたので「4÷2=2」となります。
(例2)6÷3
「÷3」は「ナイフで3つに等しく分ける」という意味でした。
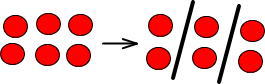
等しく2個ずつに分けられたので「6÷3=2」となります。
さて、ここからが本題です。
りんごが4個あって、そこにりんごを1個加えたとします。
これを等しく2つに分けると、どうなると思いますか。
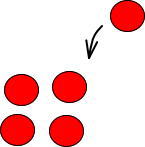
先ほどの例1を見ると、つぎのようになるとわかります。
※りんご1個だけ、2つに等しく分けられず、あまっています。このようにあまっているものを「あまり」と言います。
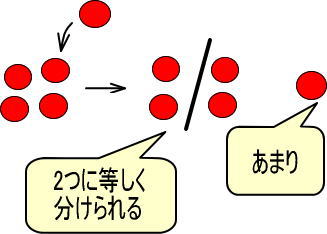
これを式で表してみましょう。
・りんご4個に1個りんごが加わったので「4+1=5」
・これを2つに等しく分けたので「÷2」
よって、「5÷2」となります。
5個のりんごを2つに等しく分けた結果、つぎのようになりました。
・等しく2個ずつに分けられた
・しかし、1個あまっている
「5÷2=2としたいところだけど、1あまっている」のようにできますよね。
個人的にはこれはこれで正しいと思いますが、数学の世界では日本語ではなく「記号」で表します。
具体的には「あまり」は「・・・」と書きます。
よって、「5÷2=2・・・1」となります。
「わかったような、わからないような…」となっているひともいると思うので、別の例をあげます。
りんごが6個あって、そこにりんごを1個加えたとします。
これを等しく3つに分けると、どうなると思いますか。
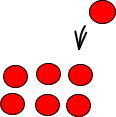
先ほどの例2を見ると、つぎのようになるとわかります。
※りんご1個あまっていますが、このようなものを「あまり」と言うのでしたね。
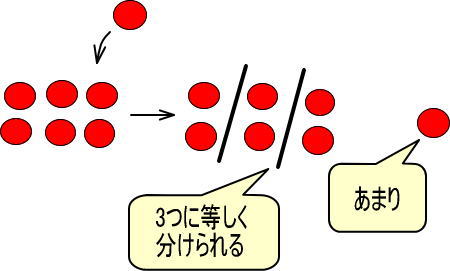
これを式で表してみましょう。
・りんご6個に1個りんごが加わったので「6+1=7」
・これを3つに等しく分けたので「÷3」
よって、「7÷3」となります。
7個のりんごを3つに等しく分けた結果、つぎのようになりました。
・等しく2個ずつに分けられた
・りんごが1個あまっている
「7÷3=2としたいところだけど、1あまっている」のようにできますね。
「あまり」は「・・・」として、「7÷3=2・・・1」となります。
スポンサード リンク
筆算であまりを出す
これからわり算の計算をする機会がありますが、たいてい図にするのは難しいので、「筆算」を使って計算します。
たとえば「51÷5」を計算する場合、「51個のりんごを5つに等しく分ける」をすぐにイメージできないので、つぎのように筆算を使って計算します。
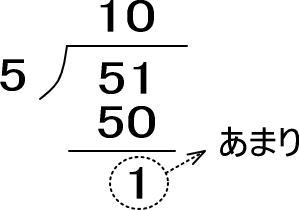
あまりは1です。
よって、「51÷5=10・・・1」となります。
このように筆算を使えば、りんごの図を描かなくても計算できてしまいますが、「あまり」がどういうものなのかしっかりイメージできないと別のところでつまづくことがあります。
りんごの図で、あまりとはどういうものなのか、しっかり理解しておきましょう。
というわけで、つぎのレッスンから、あまりのイメージについて解説していきます。