わられる数、わる数がイメージできるようになろう!
今までに学習した、わられる数、わる数のイメージです。
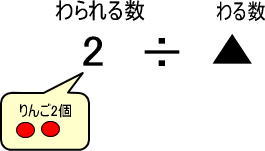
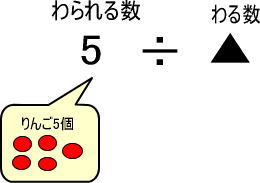
<わられる数のイメージ>
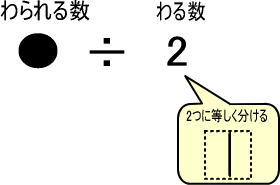
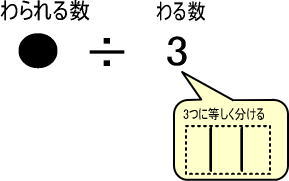
<「÷わる数」のイメージ>
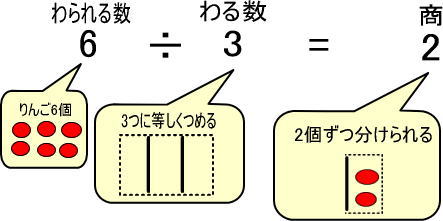
よって、「6÷3」は「6個のりんごを、3つに等しく分ける」と考えることができます。
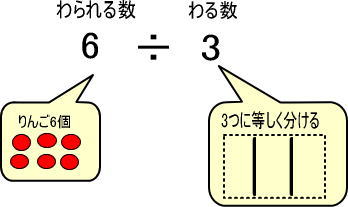
実際に、りんご6個を3つに等しく分けると、2個ずつに分けられます。
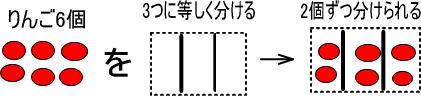
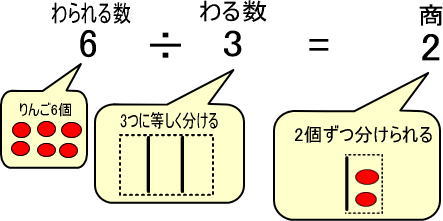
これを式にしたのが以下です。
ここまではすでに学習しましたね。
スポンサード リンク
「÷わる数」を「箱」とイメージすれば、「商」がイメージしやすくなる!
今回だけ、「÷わる数」を、つぎのように考えます。
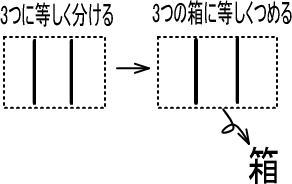
※ほかに例示します。
(例1) ÷2 → 2つの箱に等しくつめる
(例2) ÷5 → 5つの箱に等しくつめる
(例3) ÷7 → 7つの箱に等しくつめる
では、つぎの式は、どのように考えられると思いますか。
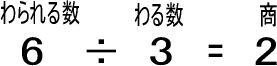
つぎのようになります。
・6 → りんご6個
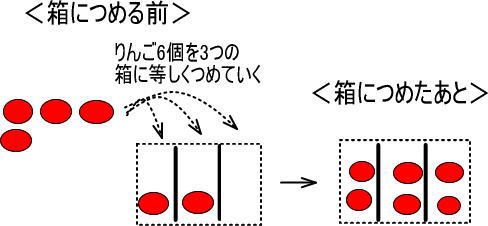
・÷3 → 今回は「3つに等しく分ける」ではなく「3つの箱に等しくつめる」と考える
・2 → 今回は「2個ずつ分けられた」ではなく、「それぞれの箱にりんご2個ずつはいっていた」と考える
つまり「りんご6個、箱が3つあった。それぞれの箱のりんごの数が等しくなるように、りんごを順に箱につめていった」「すると、それぞれの箱にりんごが2個ずつはいった」と考えます。
図にすると、つぎのようになります。
ここで質問です。
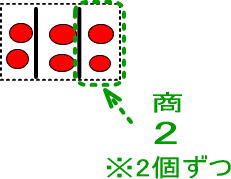
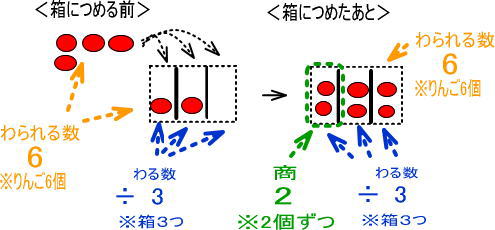
「商」の2は上図のどこだと思いますか。
商は「りんごを箱につめ終わったあと、箱にいくつずつ分けられたのか」を表しています。
すなわち、3つの箱のうち、1つの箱のりんごの数が「商」ですね。
※3つの箱はすべて等しいので、3つの箱のどの箱でもOKです。
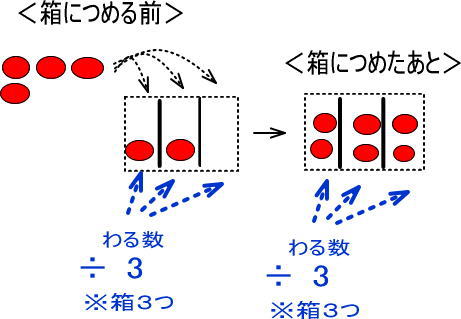
「わる数」の3は、上図のどこだと思いますか。
わる数は「箱の数」ですね。
よって、つぎのようになります。
「わられる数」の6は、上図のどこだと思いますか。
まずは、りんごを箱につめる前ですが、つぎのところですね。
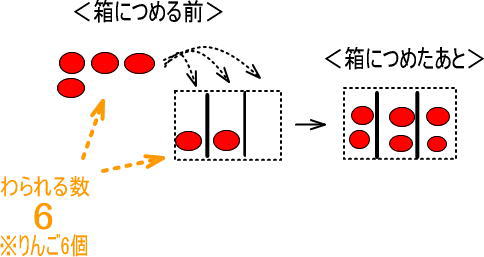
つめ終わったあと、6個のりんごはどこにあると思いますか。
あまりはない、すなわち、すべて箱につめたということなので、6個すべて3つの箱のなかにあります。
これは、案外、盲点になるので、しっかり覚えておいてください。
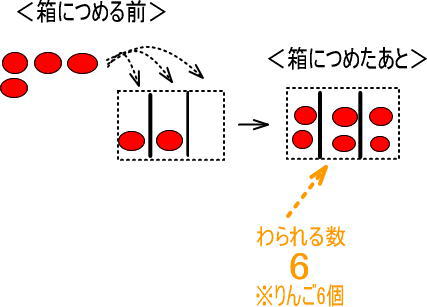
まとめると、つぎのようになります。
これを式で表すと、つぎのようになります。
「わる数」の考えかたを「箱」にしただけなので、当然、先ほどと同じ式になります。
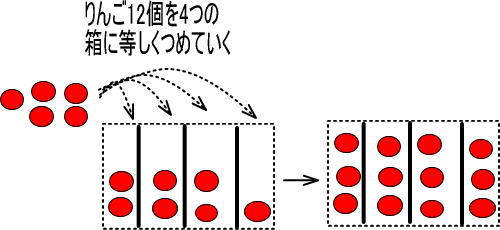
では「12÷4=3」は、どうなるでしょうか。
この式のイメージです。
・12 → りんごが12個あった。
・÷4 → それらのりんごを4つの箱に等しくつめていった。
・3 → すると、それぞれの箱にりんご3個ずつはいった。
よって、「12÷4」は、つぎのように考えることができます。
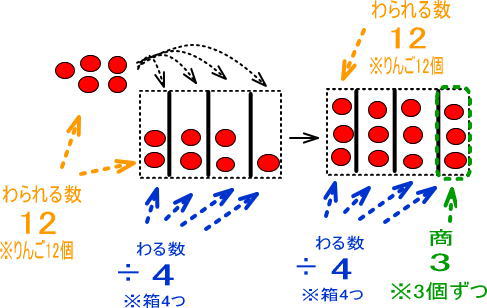
「商」は、りんごをつめ終わったあと、箱にいくつずつはいっているのかを表していました。
いま、4つの箱に、それぞれ3個ずつりんごがはいっています。
「わる数」は、箱の数でした。
いまは、4つあります。
「わられる数」は、すべてのりんごの数です。
りんごをつめたあとは、箱にすべてのりんごがはいっています。
まとめると、つぎのようになります。
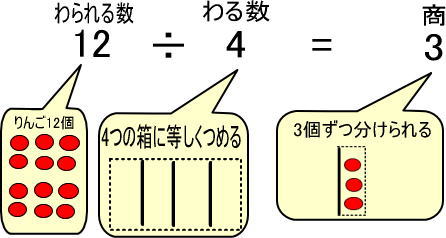
これを式で表すと、つぎのようになります。
ここまでわかれば準備は完了です。
スポンサード リンク
「(わられる数)=(わる数)×(商)」という式がでてくる理由
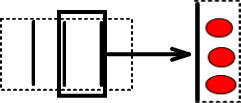
つぎの●は、いくつになると思いますか。
※「かけ算とわり算の不思議な関係」で学習したように考えても構いません。ここでは別の考えかたを紹介します。

この式のイメージです。
・● → りんごがいくつかあった。
・÷4 → それらを4つの箱に等しくつめていった
・3 → すると、それぞれの箱にりんご3個ずつはいった
りんごをつめ終わったあとの話です。
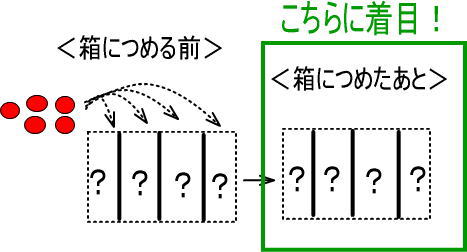
4つの箱のうち、1つの箱に着目したのが「商」でした。
いま、商は3なので、1つの箱には3個のりんごがはいっていますね。
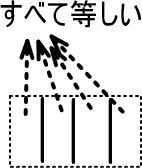
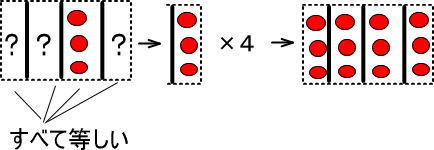
4つの箱は、すべて等しいのでした。
つまり、「3個ずつはいっている箱」を4つコピーすれば、すなわち「×4」すれば、4つの箱の中にいくつりんごが入っているのかわかります。
よって、箱のなかには「3×4=12」のりんごがあるとわかります。
さて、あまりがないように、すべてのりんご、すなわち●個のりんごを4つの箱につめました。
よって、4つの箱にすべてのりんご、すなわち●個のりんごがはいっています。
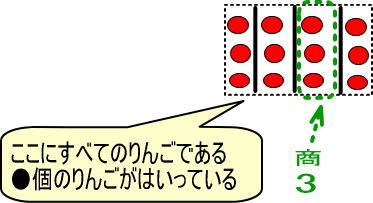
というわけで、●は「3×4=12」になります。
いままでの話がわかっていれば解けますね!
さて、ここで元の式をもう一度見てみてください。

「箱」の数は4個、それぞれの箱には3個ずつのりんごがはいっているとわかります。
よって、「商」の3を、「わる数」の4だけかけると、「わられる数」がでてくるとわかります。
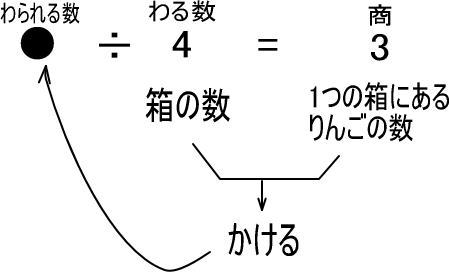
というわけで、「(わられる数)=(わる数)×(商)」という式がでてくるわけですね。
ここまで理解できれば、つぎの「あまり」はかんたんに思えるはずです!