まずは一の位のイメージをつかもう!
赤い玉を1から9個まで置くことができるカードがあります(0個もありますが、あとで説明します)。
このカードには「一の位」という名前がついています。
では、このカードに赤い玉を1個置いてみましょう。
つぎのようになりますね。
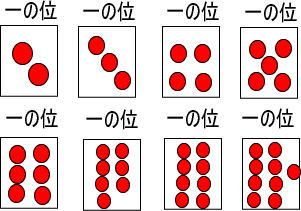
同じように、カードに赤い玉を2個、3個、4個、5個、6個、7個、8個、9個と置くと、それぞれつぎのようになりますね。
当たり前ですね。
スポンサード リンク
つぎに、十の位のイメージをつかもう!
質問です。
赤い玉が10個あります。
これらをカードに置くとどうなると思いますか。
つぎのようにしたいところですが、一の位のカードには赤い玉を1個から9個までしか置くことができません。
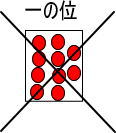
では、どのようにすればいいのでしょうか。
ここで「十の位のカード」が登場します。
十の位のカードには、黄色い玉を1個から9個まで置くことができます(0もあります)。
なお、十の位のカードは一の位のカードの左側に置きます。
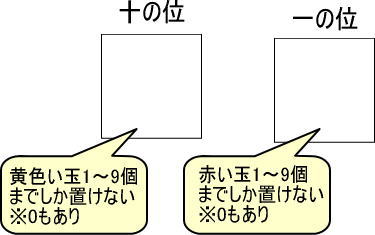
「赤い玉が10個あって、それをカードに置くんだよ?黄色い玉ってなんだ?」と思ったことでしょう。
ご安心ください。
1円玉10枚あれば10円玉1枚と交換できるのと同じで、赤い玉10個は黄色い玉1個と交換できます。
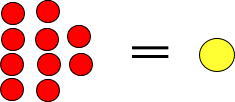
よって、つぎのようになります。
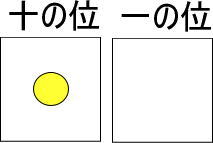
これで「黄色い玉が1個ある → 黄色い玉1個と赤い玉10個を交換できる → 赤い玉10個あるのと同じ」となります。
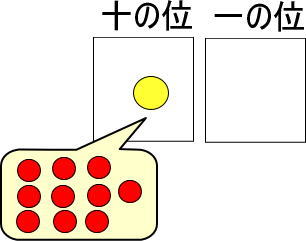
ちなみに、一の位のカードに何も書かないわけにはいかないので、「ない」ということで「0」を書きます。
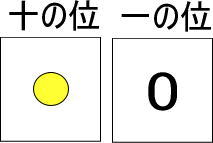
では質問です。
つぎのカードの場合、赤い玉はいくつあると思いますか?
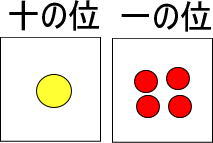
黄色い玉1個は、赤い玉10個と交換できるのですよね。
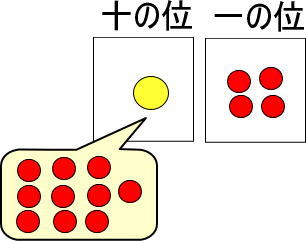
よって、「10+4」で、「14」です。
では、つぎのカードの場合、赤い玉はいくつあると思いますか?
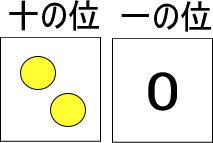
黄色い玉1個は、赤い玉10個と交換できるのですよね。
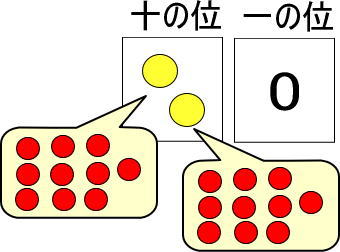
「赤い玉10個」が2つあります。
まったく同じものが2つあるわけなので、2回コピーしているのと同じです。

よって、(赤い玉10個)×2と計算できます。
「10×2」で、「20個」です。
では、赤い玉18個をカードに置いてみてください。
赤い玉18個のうち、10個は黄色の玉に交換できます。
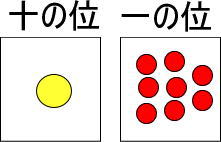
つまり、赤い玉18個は、黄色い玉1個と赤い玉8個ということですね。
よって、つぎのようになります。
スポンサード リンク
百の位も考えかたは同じ!
黄色い玉が10個あったとします。
これをカードで表すと、どうなると思いますか。
つぎのようになると考えたひともいるかもしれませんが、カードには黄色い玉を1〜9個しか置けません。
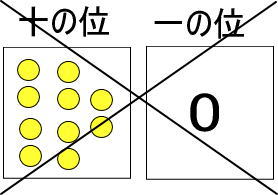
ここで「百の位のカード」が登場します。
百の位のカードには、青い玉を1から9個まで置くことができます(0もあります)。
なお、百の位のカードは十の位のカードの左側に置きます。
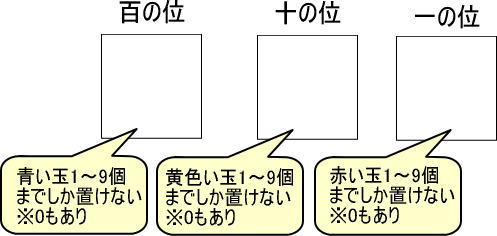
10円玉10枚あれば100円玉1枚と交換できるのと同じで、黄色い玉10個は青い玉1個と交換できます。
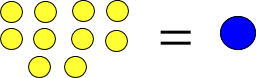
よって、黄色い玉10個ある場合は、つぎのように表すことができます。
これで「青い玉が1個ある → 青い玉1個と黄色い玉10個を交換できる → 黄色い玉10個あるのと同じ」となります。
先ほどの話と同じですね。
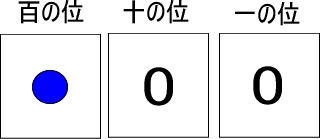
では質問です。
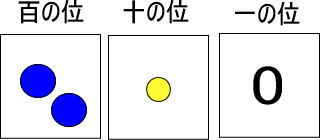
つぎのカードの場合、黄色い玉はいくつになると思いますか。
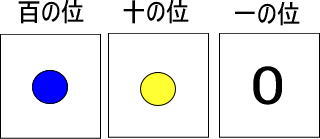
青い玉1個は、黄色い玉10個と交換できるのですよね。
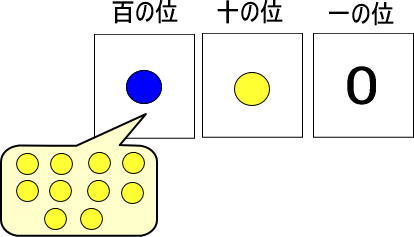
黄色い玉は「10+1」で、「11個」ですね。
では、黄色い玉21個をカードに置いてみてください。
黄色い玉21個のうち20個は、青い玉2個と交換できますよね。
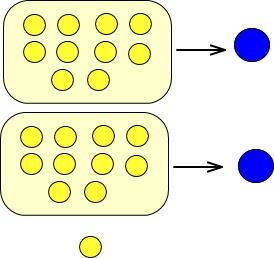
よって、つぎのようになります。
スポンサード リンク
千の位の数以降も考えかたは同じ
青い玉が10個あれば、どうなると思いますか。
いままでと同じです
「千の位のカード」がでてくるだけです。
これがずっと続いていきます。