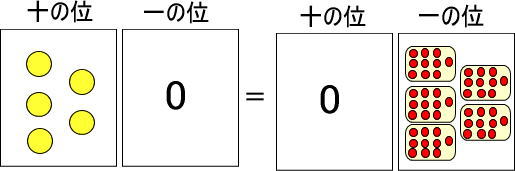
十の位は「10×黄色い玉の数」で赤い玉にできる!
十の位のカードに黄色い玉が1個あります。
これは赤い玉だと何個分になりますか。
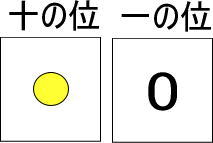
黄色い玉1個は赤い玉10個と交換できるのでしたね。
よって、赤い玉10個です。
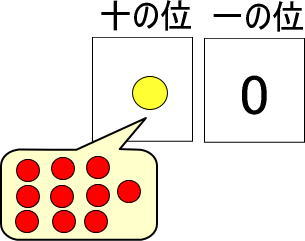
さて、ここで黄色い玉1個を赤い玉10個に交換してみます。
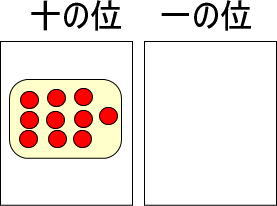
十の位には黄色い玉を置くので、赤い玉を置いてはいけませんよね。
そこで、つぎのように置きかえてみます。
※一の位のカードに置ける赤い玉は1〜9個までですが、今回だけ特別に10個置いています。
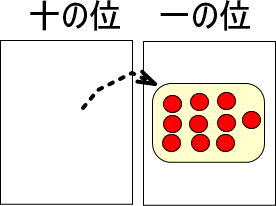
まとめると、つぎのようになります。
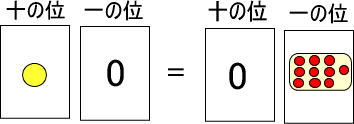
さて、質問です。
十の位のカードに黄色い玉が2個あります。
これは赤い玉だと何個分になりますか。
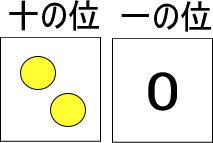
つぎのように考えることができますね。
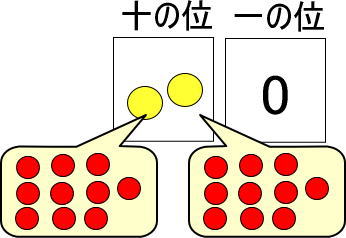
「赤い玉10個」が2つあります。
まったく同じものが2つあるわけなので、2回コピーしているのと同じです。

よって、(赤い玉10個)×2と計算できます。
「10×2」で、赤い玉は20個になります。
さて、ここで、黄色い玉を赤い玉に交換してみます。
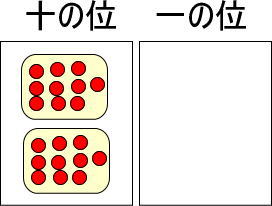
十の位には黄色い玉を置くので、赤い玉を置いてはいけませんよね。
そこで、つぎのように置きかえてみます。
※一の位のカードに置ける赤い玉は1〜9個までですが、今回だけ特別に20個置いています。
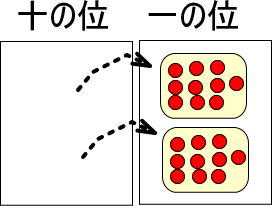
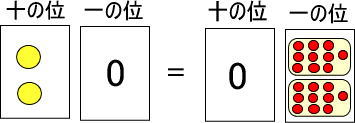
まとめると、つぎのようになります。
十の位のカードに黄色い玉が3個あります。
これは赤い玉だと何個分になりますか。
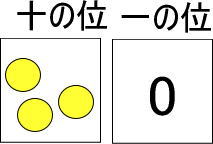
つぎのように考えることができますね。
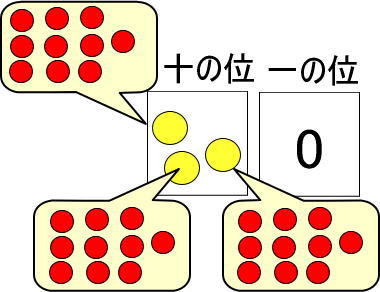
「赤い玉10個」が3つあります。
まったく同じものが3つあるわけなので、3回コピーしているのと同じです。

よって、(赤い玉10個)×3と計算できます。
「10×3」で、赤い玉は30個になります。
さて、ここで、黄色い玉を赤い玉に交換してみます。
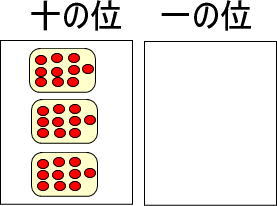
十の位には黄色い玉を置くので、赤い玉を置いてはいけませんよね。
そこで、つぎのように置きかえてみます。
※一の位のカードに置ける赤い玉は1〜9個までですが、今回だけ特別に30個置いています。
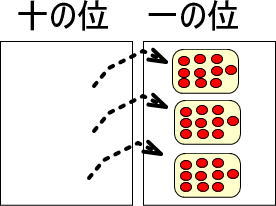
まとめると、つぎのようになります。
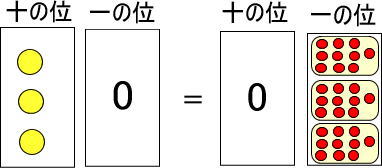
以上をまとめると、つぎのようになります。
<黄色い玉が1個の場合>

<黄色い玉が2個の場合>

<黄色い玉が3個の場合>

では、質問です。
十の位に黄色い玉が5個あった場合、赤い玉はいくつになると思いますか。
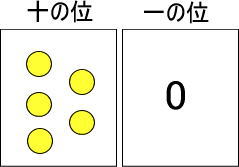
つぎのようにできると予測できますよね。
その通りです!
「赤い玉10個」が5つあるので、10×5で計算できます。
50個です。
さらに質問です。
十の位に黄色い玉が8個あった場合、赤い玉はいくつになると思いますか。
「赤い玉10個」が8つあるので、10×8で計算できるとわかりますよね。
80個です。
というわけで、つぎのようになります。
・十の位に黄色い玉1個 → 10×1
・十の位に黄色い玉2個 → 10×2
・十の位に黄色い玉3個 → 10×3
・十の位に黄色い玉4個 → 10×4
・十の位に黄色い玉5個 → 10×5
・十の位に黄色い玉6個 → 10×6
・十の位に黄色い玉7個 → 10×7
・十の位に黄色い玉8個 → 10×8
・十の位に黄色い玉9個 → 10×9
よって、十の位の黄色い玉は、「10×(黄色い玉の数)」で赤い玉の数になおすことができるとがわかります。
スポンサード リンク
十の位は「100×青い玉の数」で赤い玉にできる!
百の位のカードに青い玉が1個あります。
これは赤い玉だと何個分になりますか。
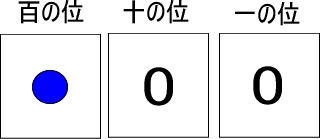
青い玉1個は、黄色い玉10個と交換できました。
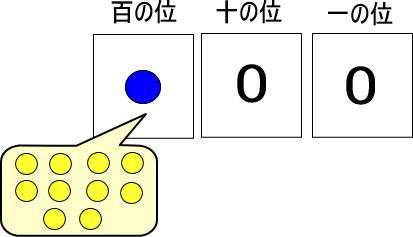
というわけで、青い玉を黄色い玉に交換します。
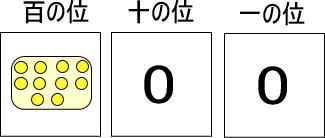
百の位には青い玉を置くので、黄色い玉を置いてはいけませんよね。
そこで、つぎのように置きかえてみます。
※一の位のカードに置ける黄色い玉は1〜9個までですが、今回だけ特別に10個置いています。
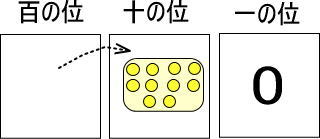
黄色い玉1個は、それぞれ赤い玉10個と交換できます。
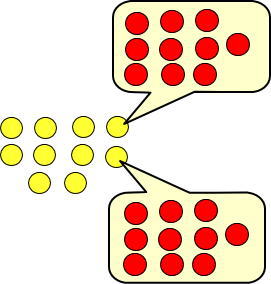
というわけで、黄色い玉を赤い玉に交換しました。
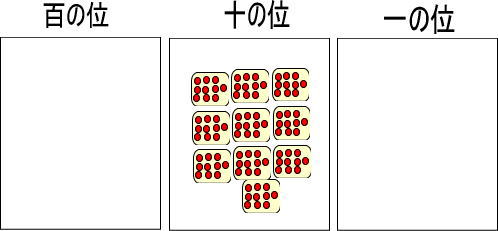
十の位には黄色い玉を置くので、赤い玉を置いてはいけませんよね。
そこで、つぎのように置きかえてみます。
※一の位のカードに置ける赤い玉は1〜9個までですが、今回だけ特別に100個置いています。
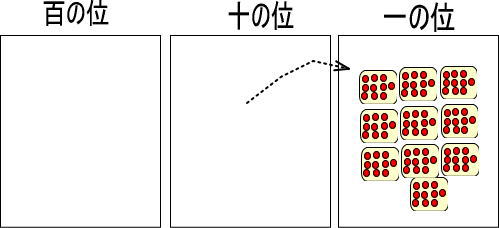
よって、つぎのように考えることができます。

「赤い玉10個」を10回コピーしているわけなので、(赤い玉10個)×10と計算できます。
よって、「10×10」で、赤い玉は100個になります。
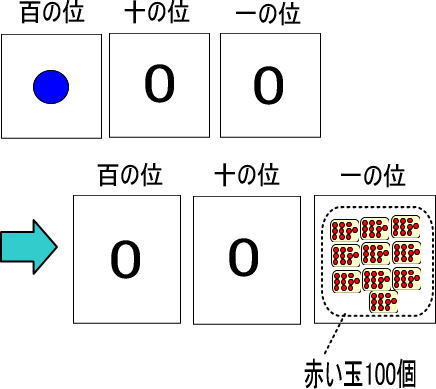
まとめると、つぎのようになります。
青い玉1個が赤い玉100個になるのですが、100円玉1枚あれば1円玉が100枚と交換できるのと同じですね。
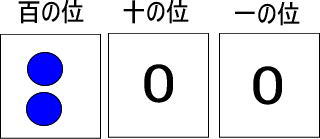
百の位のカードに青い玉が2個あります。
これは赤い玉だと何個分になりますか。
青い玉1個は、黄色い玉10個と交換できました。
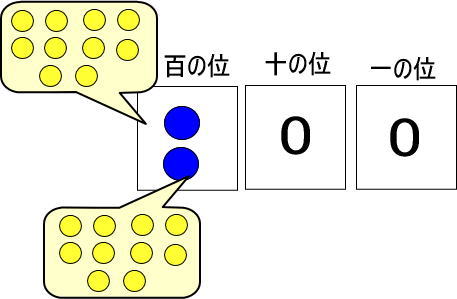
というわけで、青い玉を黄色い玉に交換します。
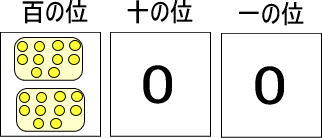
百の位には青い玉を置くので、黄色い玉を置いてはいけませんよね。
そこで、つぎのように置きかえてみます。
※一の位のカードに置ける黄色い玉は1〜9個までですが、今回だけ特別に20個置いています。
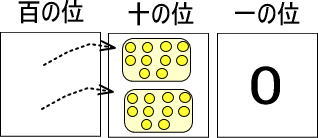
黄色い玉1個は、それぞれ赤い玉10個と交換できます。

というわけで、黄色い玉を赤い玉に交換しました。
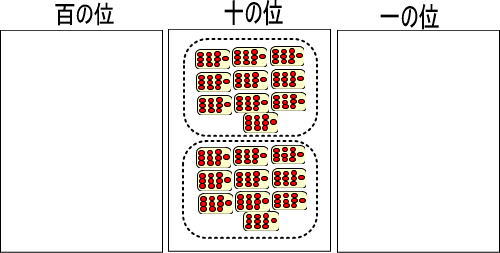
十の位には黄色い玉を置くので、赤い玉を置いてはいけませんよね。
そこで、つぎのように置きかえてみます。
※一の位のカードに置ける赤い玉は1〜9個までですが、今回だけ特別に100個置いています。
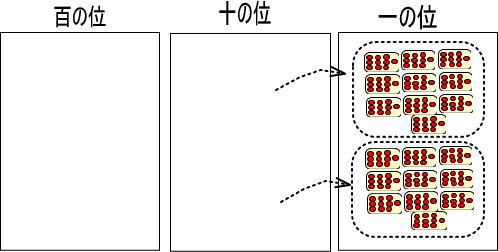
さて、ここで今までの話を思い出してください。
つぎのように考えましたよね。
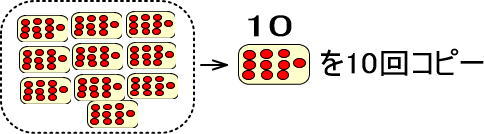
つまり、つぎのようになります。
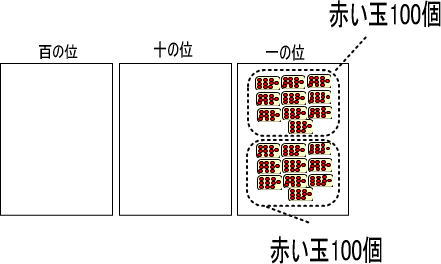
赤い玉100個が2つあるので、答えは「100×2」で、200になります。
まとめると、つぎのようになります。
青い玉2個が赤い玉200個になります。
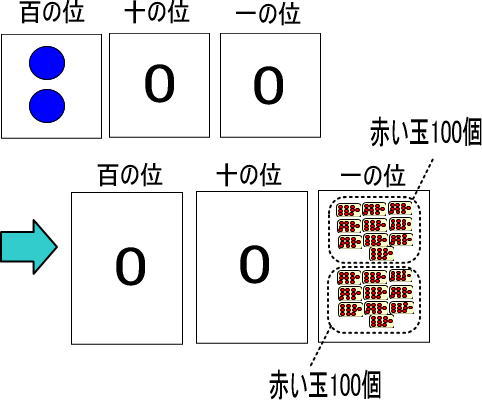
以上をまとめると、つぎのようになります。
<青い玉が1個の場合>

<青い玉が2個の場合>

では、質問です。
百の位に青い玉が3個あった場合、赤い玉はいくつになると思いますか。
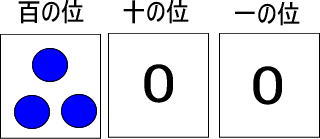
つぎのようにできると予測できますよね。
その通りです!
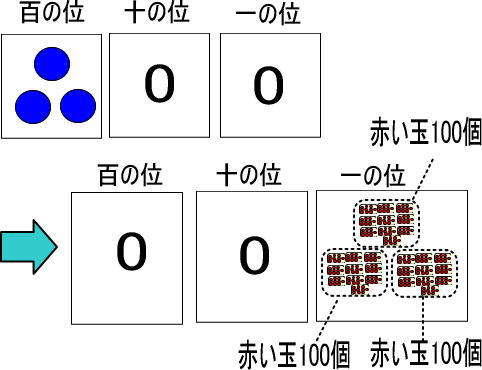
「赤い玉100個」が3つあるので、100×3で計算できます。
300個です。
さらに質問です。
百の位に青い玉が5個あった場合、赤い玉はいくつになると思いますか。
「赤い玉100個」が5つあるので、100×5で計算できるとわかりますよね。
500個です。
というわけで、つぎのようになります。
・百の位に青い玉1個 → 100×1
・百の位に青い玉2個 → 100×2
・百の位に青い玉3個 → 100×3
・百の位に青い玉4個 → 100×4
・百の位に青い玉5個 → 100×5
・百の位に青い玉6個 → 100×6
・百の位に青い玉7個 → 100×7
・百の位に青い玉8個 → 100×8
・百の位に青い玉9個 → 100×9
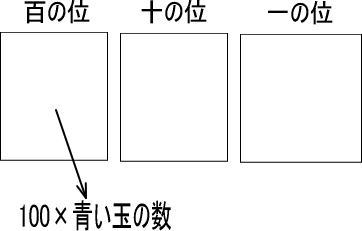
よって、百の位の青い玉は、「10×(青い玉の数)」で赤い玉の数になおすことができるとがわかります。
スポンサード リンク
すべての玉を赤い玉に交換してみよう!
つぎのカードの玉をすべて赤い玉にすると、いくつになりますか。
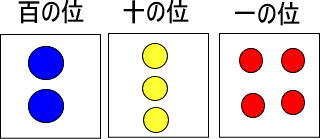
まずは百の位だけに着目します(つぎのように手で隠すといいですよ)。
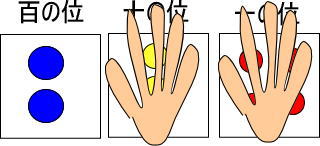
青い玉が2個あるので、赤い玉は「100×2」で200個ですね。
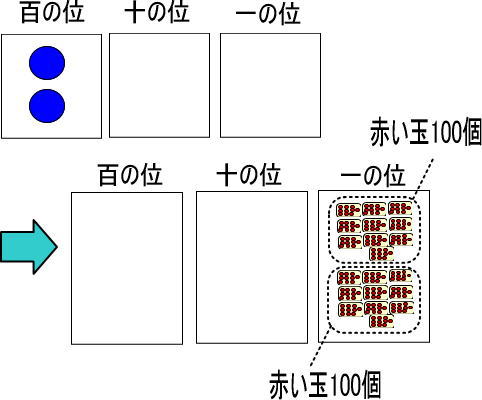
つぎに十の位だけに着目します。
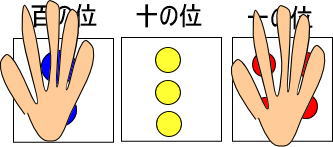
黄色い玉が3個あるので、赤い玉は「10×3」で30個ですね。
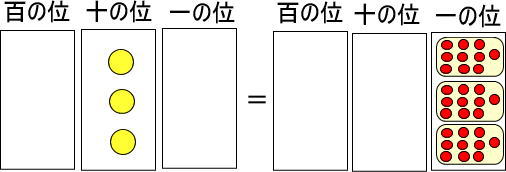
最後に一の位だけに着目します。
赤い玉が4個ありますね。
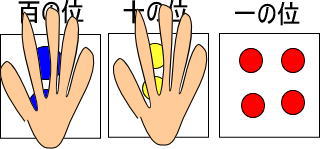
よって、「200+30+4」で「234」になります。