がい数とは、およその数、だいたいの数
「お年玉を、18893円もらった」と言われても、どのくらいの金額なのか、パッと理解できないと思います。
一方、「お年玉は、だいたい、2万円くらいだった」「お年玉は、およそ2万円だった」と言われると、どのくらいの金額なのか、すぐにわかるのではないでしょうか。
だから、日常生活では、「だいたい」「およそ」という言葉は、よく使われます。
(例1)買い物の代金は、およそ3千円だった(本当は2874円)。
(例2)駄菓子は全部で、だいたい500円だった(本当は479円)
「だいたいの数」「およその数」のことを「がい数」といいます。覚えておきましょう。
(本当の数)11345 → だいたいいくつなのかイメージしにくい
(がい数)11000 → 正確ではないのですが、いくつなのか、およそのイメージがわかる
ここで疑問に思ったひともいると思います。
先ほどの例で、つぎのようにしてはいけないのか、という疑問です。
(本当の数)11345
(がい数)11000 → 「10000」だと間違いなの?「11300」だと間違いなの?
結論からいえば、すべて正解です。
よって、がい数を求める問には、たいてい、答えがひとつになるように指示されています。具体的には、つぎのように「位の数」についての指示がつきます。
スポンサード リンク
「●の位までのがい数」と指示があれば、一桁下を四捨五入!
まずは「●の位までのがい数」という指示からです。
このように指示されれば、一桁下を四捨五入すればいいのですが…。どういうことかわからないと思うので、例題を通して説明します。
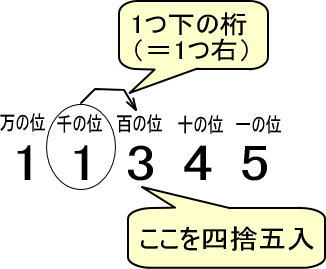
(例)11345を千の位までのがい数にしてください。
この指示、わかりにくいですよね。
そこで、慣れるまではつぎのように考えるといいでしょう。
1.位の数を書きこみます。
※右から順に「一の位」「百の位」「千の位」「万の位」となります。

2.問に「千の位」とあるので、千の位に〇をつけます。

3.〇をつけた位の数よりも、1つ下の位(つまりすぐ右にある位の数のこと)を四捨五入します。
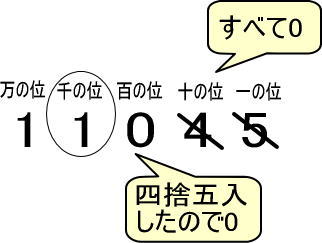
4.四捨五入した位の数よりも下の位(四捨五入した位の数よりも右の位の数)はすべて「0」にします。
百の位を四捨五入しました。
百の位よりも下の位、つまり百の位よりも右にある十の位、一の位の両方を「0」にします。
※四捨五入とは?
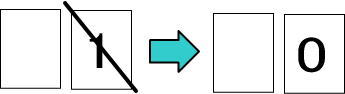
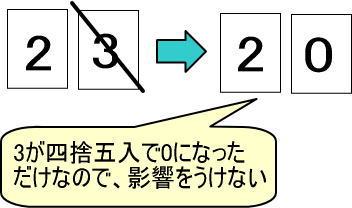
・1から4までの数は切り捨てします。要は、1から4までの数なら「0」にします。
(例1)
(例2)
(例3)
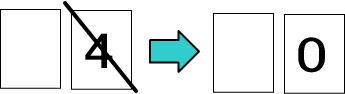
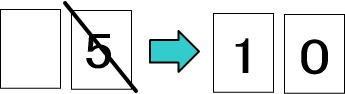
・5から9までの数は繰り上げします。要は、5から9なら、ひとつ位が上の数に「1」を加えます。
(例1)
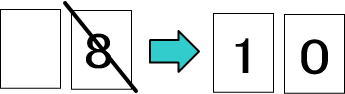
(例2)
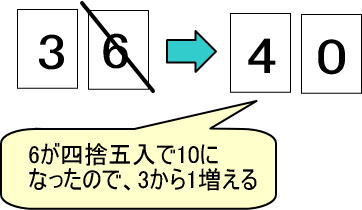
(例3)
よって、答えは「11000」です。
「11345のがい数は?」と聞かれると、「11000」「10000」「11300」など、いくつも答えがでてきますが、「千の位までのがい数」と聞かれると「11000」だけになりますね。
「上から●桁のがい数」と指示があれば、一桁下を四捨五入!
「上から●桁のがい数」という指示もあります。
このように指示された場合、1桁下を四捨五入しますが…。よくわからないと思います。そこで、例題を通して説明します。
(例)11345を上から2桁のがい数にしてください。
1.指示されている桁数に□をつけます。
※「上から2桁」については、すでに学習しています。

2.□から1桁下を四捨五入します。

「3」を四捨五入すればいいのですね。
四捨五入すれば「0」です。
3.四捨五入した位の数よりも下の位(四捨五入した位の数よりも右の位の数)はすべて「0」にします。
百の位を四捨五入しました。
百の位よりも下の位、つまり百の位よりも右にある十の位、一の位の両方を「0」にします。
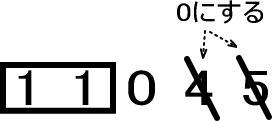
よって、答えは「11000」になります。