(速さ)は(道のり)÷(時間)で計算できる!
(問)A町からB町まで12kmあります。太郎君はA町からB町まで3時間で歩きました。時速何kmで歩きましたか。
このような速さに関する問題は、まずは「地図」を描きます。
地図といっても、横線だけのかんたんなものでいいのですが…。はじめのうちはどのような地図を描けばいいのかわからないと思うので、ていねいに説明します。
まずは横線を一本ひきます。
![]()
つぎに、この線に「場所」「道のり」を書きこみます。
具体的には、場所としてA町とB町、道のりとして12kmを書きこみます。

つぎに、登場人物と「速さ」を書きこみます。
今回の問では、速さを求めるので「?」としています。
最後に「時間」を書きこみます。
なお、下図では、解説しやすいように時間を書きこみましたが、どこからどこまでの時間かわかるようにすれば、どのように書いても構いません。
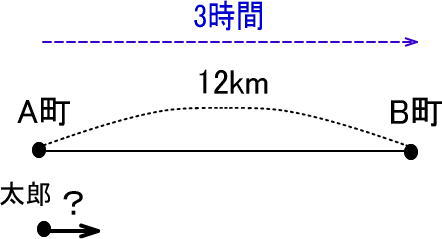
まとめると、地図を描くとき、横線を引いて、つぎの3つを書きこみます。
・場所と道のり
・時間
・登場人物の速さ(これを求めるので今回は「?」としています)
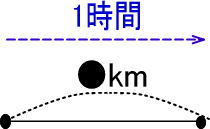
さて、いま、太郎君は時速何kmで歩いたのかを求めたい、言いかえると、太郎君は「1時間で何km歩いたのか」を求めたいのですね。
図で表すと、つぎのようになります。
※もしこれがわからないのなら、前のレッスンを読みなおしてください。
ここで地図をつぎのように工夫してみます。
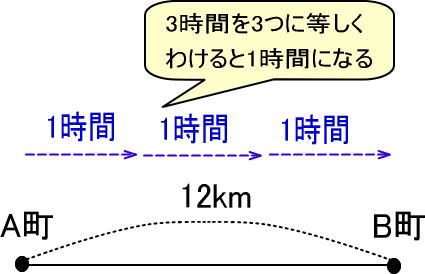
すると、太郎君は1時間で何km歩いたのかがわかるのではないでしょうか。
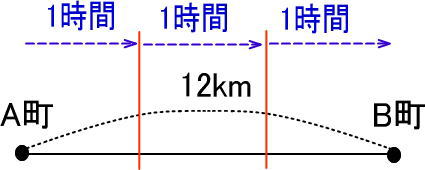
「12÷3」で、4ですね。
よって、太郎君は1時間で4kmの速さで歩いたとわかります。時速4kmですね。
さて、ここで今までの話を別の角度からみてみます。
12は「12km」の12ですね。
3は「3時間」の3ですね。
つまり、「12÷3」は、(道のり)÷(時間)で計算したのだとわかります。
よって、(速さ)=(道のり)÷(時間)で計算できそうですが…。本当でしょうか。
別の問を解いてみましょう。
(問)家からA町まで20kmあります。花子さんは4時間で歩きました。時速何kmで歩きましたか。
このような速さに関する問題は、まずは「地図」を描きます。書くべきものはつぎの3つでした。
・場所と道のり
・時間
・登場人物の速さ(これを求めるので今回は「?」としています)
というわけで、つぎのようになります。
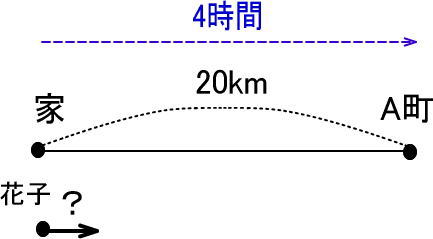
さて、いま、花子さんは時速何kmで歩いたのかを求めたい、言いかえると、花子さんは「1時間で何km歩いたのか」を求めたいのですね。
図で表すと、つぎのようになります。
※もしこれがわからないのなら、前のレッスンを読みなおしてください。

ここで地図をつぎのように工夫してみます。
すると、花子さんは1時間で何km歩いたのかがわかるのではないでしょうか。
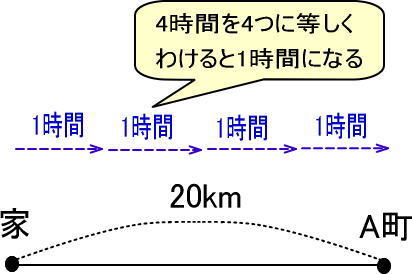
「20÷4」で、5ですね。
よって、花子さんは1時間で5kmの速さで歩いたとわかります。時速5kmですね。
さて、ここで今までの話を別の角度からみてみます。
20は「20km」の20ですね。
5は「5時間」の5ですね。
つまり、「20÷5」は、(道のり)÷(時間)で計算したのだとわかります。
よって、(速さ)=(道のり)÷(時間)で計算できそうです。
くどいですが、最後にもう一問解いてみましょう。
(問)花子さんは、家からA駅まで20分かけて歩いています。家からA駅まで1600mあるときの花子さんの速さを求めてください。
先ほどと同じように、まずは「地図」を描きます。地図にはつぎの3つを書きこむのでした。
・場所と道のり
・時間
・登場人物の速さ(これを求めるので今回は「?」としています)
よって、つぎのようになります。
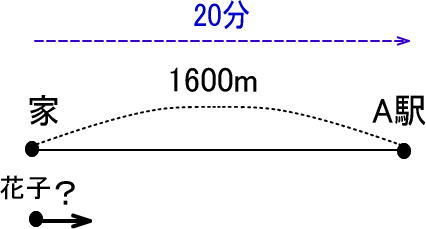
さて、いま、花子さんは分速何mで歩いたのかを求めたい、言いかえると、花子さんは「1分間で何m歩いたのか」を求めたいのですね。
これを図で表すと、つぎのようになります。
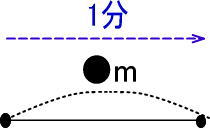
ここで先ほどの地図をつぎのように工夫してみます。
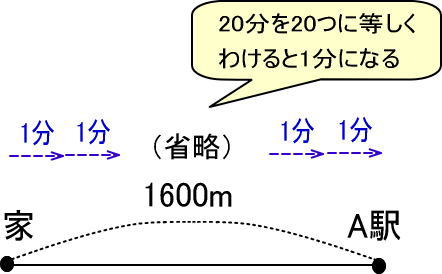
※図では省略していますが、実際は「1分」は20つあります。
すると、花子さんは1分で何m歩いたのかがわかるのではないでしょうか。
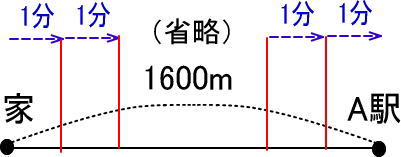
「1600÷20」で、80ですね。
よって、花子さんは1分で80mの速さで歩きました。分速80mですね。
さて、ここで今までの話を別の角度からみてみます。
1600は「1600m」の1600ですね。
20は「20分」の20ですね。
よって「1600÷2」は(道のり)÷(時間)なので、やはり、(速さ)=(道のり)÷(時間)で計算できそうですね。
つぎのレッスンに続きます。
スポンサード リンク
(参考)「比」で考えることもできる!
先ほどの例題ですが、つぎのように「比」で考えることもできます。
※比については今後説明します。たぶん。
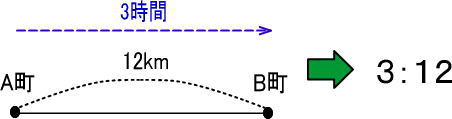
<太郎君>
・3時間で、12km歩いた
→3時間につき12km
→3:12
<速さの定義>
1時間で、何km進むのか
→1時間につき、●km進む
→1:●
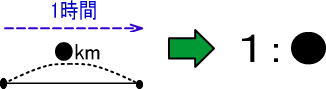
同じ「時間」と「道のり」なので、「3:12=1:●」とできます。
これを解くと、●=4と、先ほどと同じ答えになります。