速度の文章題は、まずは単位の統一!
(問)太郎君は、120分で10km歩いた。太郎君の歩く速度は、時速何kmでしょうか。
速度の問題は2ステップで解くのでした。
<STEP1>地図を描く
まずはつぎのような地図を描きます。
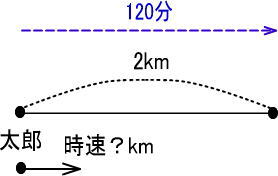
<STEP2>「きはじの図」に数値をあてはめる
そのまま「きはじの図」に数値をあてはめると、つぎのようになりますよね。
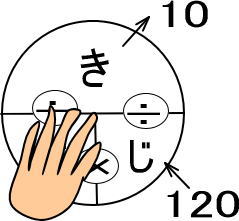
よって、答えは「10÷120」で…としてはいけません(間違いです)。
なぜ、間違いなのでしょうか。
それは単位を統一していないためです。
どういうことでしょうか。
問をもう一度よく見てください。
時速●kmなのかを計算しなければならないのですよね。
時速●kmとは「1時間で●km進む」という意味なので、「時間」と「km」で計算しますが、先ほどは「120分」「10km」と、「分」「km」で計算しました。
だから、間違いなのです。
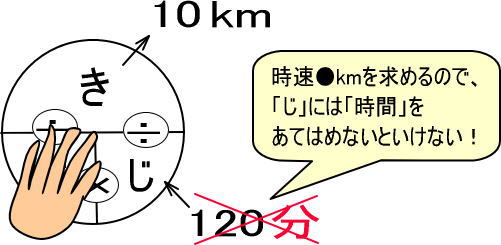
いままで「速度の文章題は2ステップで解く」と書いてきましたが、実のところ、あらたに「単位の統一」のステップを加えて、3ステップで解かなければなりません。
どういうことでしょうか。
ふたたび問を解いてみます。
<ステップ1>単位を統一します。
時速何kmなのかを求めたいのですよね。
時速●kmとは「1時間で●km進む」という意味で「時間」と「km」で計算するため、問にある時間と距離(道のり)を「時間」「km」にします。
・10km→kmなのでそのままでOK
・120分→2時間
※この計算方法についてはすでに学習しています。忘れていればしっかりと復習してください。
これからは、このような、求めたいものに応じて単位を統一するステップを加えます。
あとは、いままでと同じ手順です。
<STEP2>地図を描く
つぎのような地図になりますよね。
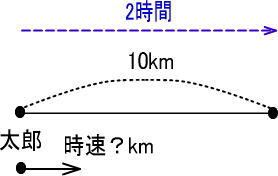
<STEP3>「きはじの図」に数値をあてはめる
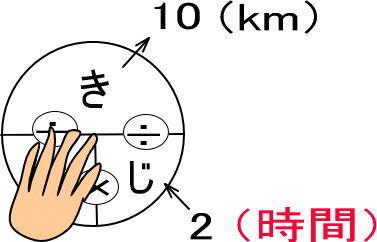
よって、答えは「10÷2」で、時速5kmです。
まとめます。
速度は、つぎのような「セット」になっています。
・時速●kmとは「1時間に●km進む」という意味 → 「時速●km」「時間」「km」がセット
・分速●mとは「1分間に●m進む」という意味 → 「分速●m」「分」「m」がセット
・秒速●mとは「1秒間に●m進む」という意味 → 「秒速●m」「秒」「m」がセット
そこで、慣れないうちは、つぎのように「求めたいもの」に応じて単位を統一するといいでしょう。
<速度を求める場合>
・時速何kmなのか求めるケース
「時速●km」「時間」「km」がセット → 問を解くまえに「時間」「km」に統一する
・分速何mなのか求めるケース
「分速●m」「分」「m」がセット → 問を解くまえに「分」「m」に統一する
・秒速何mなのか求めるケース
「秒速●m」「秒」「m」がセット → 問を解くまえに「秒」「m」に統一する
<時間を求める場合>
・何時間なのか求めるケース
「時間」は「時速●km」「km」とセット → 問を解くまえに「時速●km」「km」に統一
・何分なのか求めるケース
「分」は「分速●m」「m」とセット → 問を解くまえに「分速●m」「m」に統一
・何秒なのか求めるケース
「秒」は「秒速●m」「m」とセット → 問を解くまえに「秒速●m」「m」に統一
<距離(道のり)を求める場合>
・何kmなのか求めるケース
「km」は「時速●km」「時間」とセット → 問を解くまえに「時速●km」「時間」に統一
・何mなのか求めるケース
「m」は「分速●m」「分」とセット → 問を解くまえに「分速●m」「分」に統一
もしくは、「m」は「秒速●m」「秒」とセット → 問を解くまえに「秒速●m」「秒」に統一
※どちらなのかはケースバイケースです。
では、問を解いてみましょう。
(問)ある乗り物は、40秒で2km進んだ。秒速何mでしょうか。
<STEP1>単位を統一する
秒速何mなのかを求めます。
秒速●mは「1秒間で●m進む」という意味なので、単位を「秒」「m」に統一します。
・40秒 → 秒なのでそのまま
・2km → 2000m
<STEP2>地図を描く
つぎのような地図になりますよね。
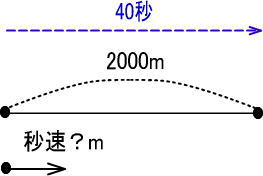
<STEP3>「きはじの図」に数値をあてはめる
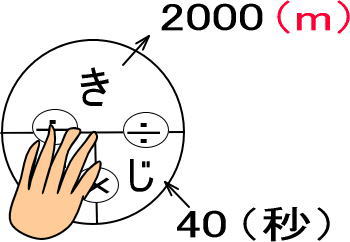
よって、答えは「2000÷40」で、秒速50mです。
<参考>単位を統一するタイミングについて
単位を統一するタイミングは、かならずしも最初(STEP1)である必要はありません。むしろ、最初に単位を統一すると計算が複雑になるケースもあります(後述します)。とはいえ、苦手なうちは単位の統一をし忘れたり、ミスしたりすることも多いので、最初に単位の統一をしています。
スポンサード リンク
単位に気をつけて、速度の文章題を解いてみよう!
(問)6kmを2時間で歩いた。分速何mでしょうか。
<STEP1>単位を統一する
分速何mなのかを求めたいのですね。
分速●mとは「1分間で●m進む」という意味なので、「分」「m」で計算します。
よって、問の単位を「分」「m」で統一します。
・6km → 6000m
・2時間 → 120分
<STEP2>地図を描く
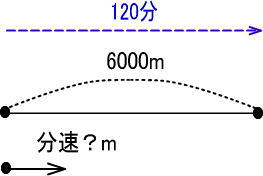
<STEP3>「きはじの図」にあてはめる
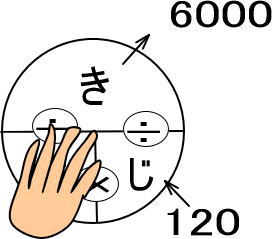
答えは「6000÷120」で、分速50mです。
では、つぎの問を解いてください。
(問)分速600mで200m走るのに、何秒かかりますか。
<STEP1>単位を統一する
何秒なのか求めたいのですよね。
「秒」は「秒速●m」「秒」とセットなので、問を「秒速●m」「m」にします。
・200m → すでにmなのでそのままでOK
・分速600m → 秒速10m
※分速●mから秒速●mへの換算方法は前のレッスンで学習しています。もし換算できないのなら、前のレッスンをしっかり復習してください。
<STEP2>地図を描く
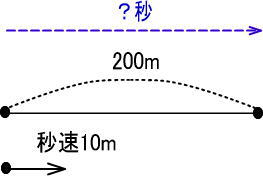
<STEP3>「きはじの図」にあてはめる
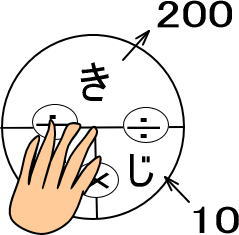
よって、答えは「200÷10」で20秒です。
<参考>
この問は、つぎのように解いたほうが楽に計算できます。
<STEP1>地図を描く
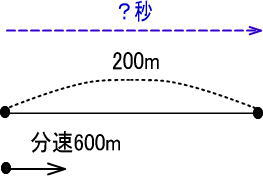
<STEP2>「きはじの図」にあてはめる
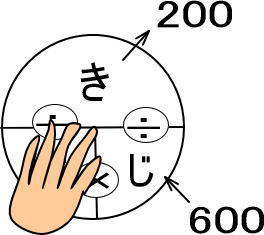
よって、「200÷600」で、1/3分です。
<STEP3>求めるものに単位を変える
求めたいのは「秒」です。
そこで、1/3分を秒にします。
よって、答えは「1/3×60」で、20秒です。
先ほどと同じ答えになりますし、先ほどよりも楽に計算できました。
どうすれば楽に計算できるのかはそのうち自然にわかるようになるので、いまは多少計算が複雑になってもSTEP1で単位の統一をすることをおすすめします。