素因数分解をしてみよう！

素因数分解してみよう！

（例題1）108を素因数分解してください。

「素因数分解とは？」のページで解説した方法だと、108をかけ算の形にして――。
※ただし「×1」を使わない

「2×54」
→まだ54はかけ算の形にできる！
※ほかにも、「3×36」「9×12」などと形がちがっても結果は同じになります。

「2×2×27」
→まだ27はかけ算の形にできる！

「2×2×3×9」
→まだ9はかけ算の形にできる！

「2×2×3×3」
→これ以上できない。

よって、答えは「2×2×3×3」。
※実際の答えは、累乗にしてください。ネットでは累乗を表しにくいため、かけ算の形にしていますが、答案だと×にされてしまいます。

これで素因数分解することもできますが、素因数分解する数の桁数が多ければ少ししんどいです。

そこで、今回は別の方法である「はしご算」を紹介します。
※今回の勉強をする前に、素数だけではなく、「割り切れるかどうかを判断する方法」のページもしっかりと読んでおいてください。

素因数分解は「はしご算」

（例題1）108を因数分解してください（ただし、はしご算を使ってください）

これから、1つずつ、ゆっくりと解説してきますが、実際に手を動かさないと、身につきません！
一緒に紙に書いてみてください！


（１）まずは、素因数分解する数を紙に書きます。




（２）（１）の数字に、わり算の「逆」の線を書きます。




（３）１０８を割れる数を考えてみてください（つまり、「１０８÷●」が割り切れるときの●のこと）。２、３、９など、いくつか数が思いつくはずです。これらの数のうち、もっとも小さい素数を１０８の隣に書きます。今の場合は「２」ですね。
※このとき、「割り切れるかどうかを判断する方法」の知識が役立ちます。




（４）１０８を（３）で書いた数で割ってください。つまり、１０８を２で割るわけですね。わり算の結果をその下に書きます。これはわり算と同じですね（わり算を逆にしただけ）。




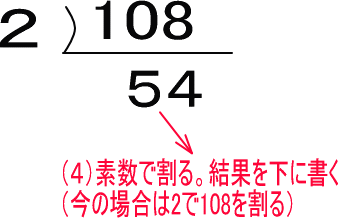
（５）５４にも、わり算の「逆」の線を書きます。




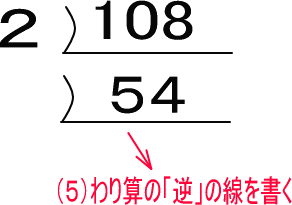
（６）５４は２で割れそうです。そこで、図のように２を下にも書きます。




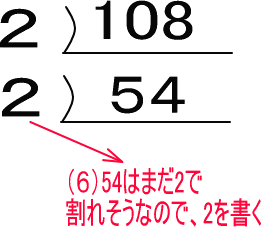
（７）５４を２で割った結果を下に書きます。５４を２で割ると２７。その２７を書くわけですね。これもわり算と「逆」に書くと考えるといいでしょう。




（８）２７にも、わり算の逆の線を書きます。

…いつまでこういう線を引くのかって？
割れる数がなくなるまでやっていきます！




（９）（６）と同じです。２をそのまま下に書くのですが…。２７は２で割ることができません。




（１０）（９）のように割れない場合は、つぎの2つの条件の両方ともにあう数を書きます。

・今までの手順で使ってきた素数（今の場合は2）よりも大きな素数
・計算結果の数（今の場合は27）を割ることができる数

3ですね。




（１１）3で27を割ります。これは今までの手順と同じです。




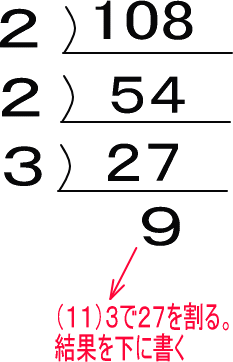
（１２）わり算と逆の線を書きます。




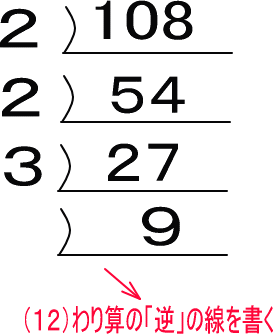
（１３）9は3で割れそうなので、3を書きます。




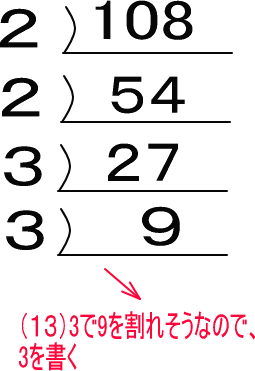
（１４）9を3で割って結果を下に書きます。これ以上、割ることができないので、終わりです（まだ3で割ることができますが、1になるまで割る必要はありません）。




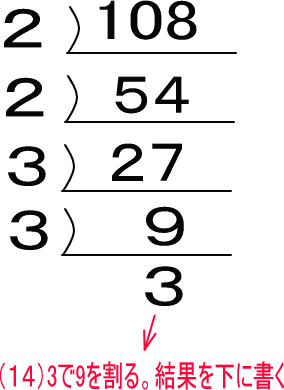
（１５）図の部分をかけ算にしたものが答えです。今の場合だと「2×2×3×3×3」ですね（実際は累乗の形にしてください）。
前のページで学習した簡易的な方法と同じ答えになりますね。

素因数分解のコツ（もっとも泥臭い方法）

素因数分解をするには、常にどの数だと割り切れるのかを考える必要があります。

たとえば、つぎのシーン。
108を割れる素数は何なのか考える必要に迫られます。




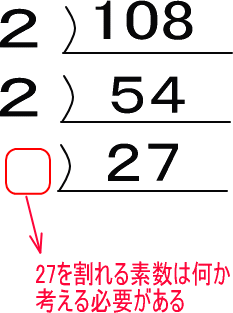
つぎに、つぎのシーン。
27を割れる素数は何なのかを考える必要に迫られます。




慣れれば簡単なのですが、慣れるまでは、つぎのようにするといいでしょう。

１．素数を、左から順に、小さな順で書いていく（「抜け」がないようにするため）
（例）2、3、5、7、11、13…

２．実際に素数で割ってみる。ただし数が小さな順。すなわち、1で書いた素数の左から順に割っていきます。

（例1）108はどの素数で割り切れる？
一番小さな素数である「2」で割ってみる！　→　108÷2＝割り切れる！

（例2）27はどの素数で割り切れる？
一番小さな素数である「2」で割ってみる！　→　27÷2＝割り切れない！　→　つぎに小さな素数である「3」で割れるかチャレンジ！　→　27÷3＝割り切れる！

これがもっとも泥臭い方法です。

素因数分解のコツ（慣れてくればこの方法で！）

慣れてくれば割り切れるかどうかを判断する方法で、どの素数だと割れるのかを判断すればいいでしょう。

（例1）291は何で割り切れる？

一番小さな素数「2」からスタート。1の位が偶数なら2で割り切れるが、291の1の位は「1」で、偶数ではない　→　2で割り切れない！　→　2のつぎに小さな素数は「3」　→　各桁の数を足すと、3で割り切れる数になれば3で割り切れる　→　「2＋9＋1＝12」。12は3で割り切れるから、291も3で割り切れる！

しかし、たとえば49のように割り切れるかどうかを判断する方法ではわからない数もあります。
その場合は、2、3、5の次の素数である「7、11、13、17」で実際にわり算をしてみるといいでしょう。

（例2）49は何で割り切れる？
2、3、5では割り切れない！　→　7で実際にわり算をしてみる！　→　49÷7＝7　→　7で割り切れる

（例3）121は何で割り切れる？
2、3、5では割り切れない！　→　7で実際にわり算をしてみる！　→　121÷7＝割り切れない（この際、つぎの図のように実際に計算してみるといいでしょう）。



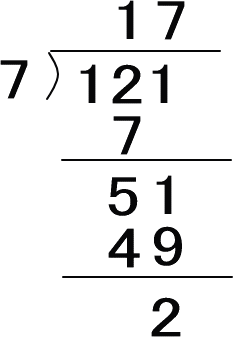
→つぎの11で割ると割り切れる！（121÷11＝11）

実はもっと効率的な方法があります。
ただ、この効率的な方法だと暗記すべきものが増えるので、数学が得意になってから覚えるといいでしょう（先ほどの問は「11の2乗＝121」を覚えていれば一発で解けます）。

今度は自分の手で素因数分解してみよう！

つぎの数を素因数分解してください。
１．６
２．１８
３．３６
４．３０
５．２０
６．７２
７．１００
８．１４
９．１０５
１０．９１

ちなみに、中には、はしご算を使わなくても解けてしまう問題もありますが、はしご算の練習のために、はしご算を使って計算してみてください。

解答

解答です。
解説は１０以外は省略していますが、わからなければ、例題2をしっかりと読んだ上、例題1の108を何度も素因数分解するといいでしょう。具体的な素因数分解の方法がわかるようになります。
※実際は、累乗の形にしてください。ネットでは累乗にしにくいのでかけ算の形にしているだけです。

１．２×３
２．２×３×３
３．２×２×３×３
４．２×３×５
５．２×２×５
６．２×２×２×３×３
７．２×２×５×５
８．２×７
９．３×５×７
１０．７×１３（2、3、5と小さな素数で割っていっても割り切れません。そこで、ためしに7で割ると、割り切れるとわかります）