あまりをイメージできるようになろう!
※先に、「箱」をイメージすれば「(わられる数)=(わる数)×(商)」の式がわかる!から読んでください。
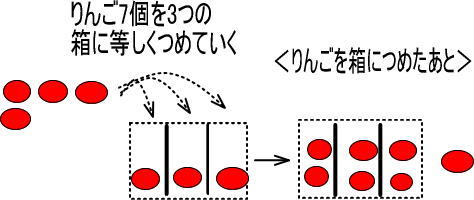
「7÷3=2・・・1」は、つぎのようにイメージできました。
・7 → りんごが7個あった
・÷3 → それらのりんごを3つの箱に等しくつめていった
・2 → それぞれの箱に2個ずつのりんごがはいった
・1 → りんごが1個あまった
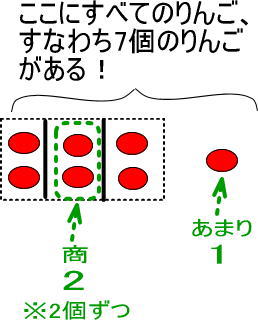
図にすると、つぎのようになります。
さて、ここで質問です。
「商」と「あまり」は上図のどこだと思いますか。
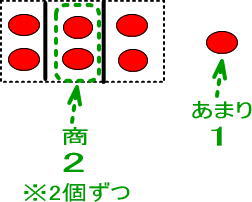
りんごを箱につめたあと、それぞれの箱にいくつりんごがはいっているのかを表しているのが「商」でした。
いま、3つの箱のうち、1つのりんごには2個のりんごがはいっています。
よって、商は2ですね。
また、りんごを箱につめたあと、あまったりんごのことを、あまりというのでした。
よって、あまりは1ですね。
まとめると、つぎのようになります。
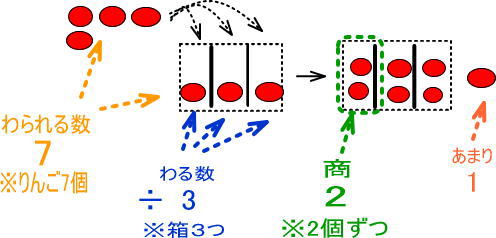
よって、つぎのようになります。
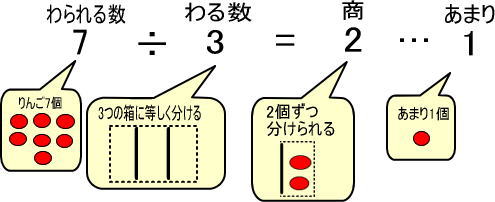
これを式で表すと、つぎのようになります。
最後に、ひとつ質問です。
つめ終わったあと、すべてのりんご(いまの場合は7個のりんご)は、どこにありますか。

つぎのようになりますね。
※詳しくいうと「箱にはいっているりんごすべて」と「あまったりんご」の合計です。
今までの復習がしっかりできていれば、ここまではわかると思います。
スポンサード リンク
(わられる数)=(わる数)×(商)+(あまり) の式がでてくる理由
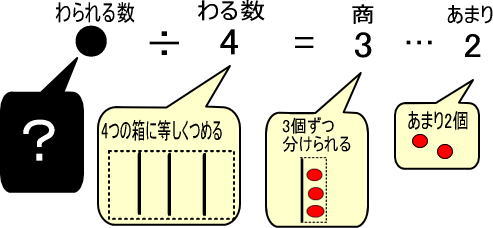
つぎの●は、いくつだと思いますか。
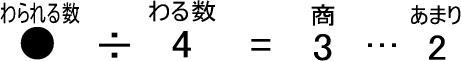
この式のイメージです。
・● → りんごがいくつかあった
・÷4 → それらを4つの箱に等しくつめていった
・3 → すると、それぞれの箱にりんご3個ずつはいった
・2 → りんごが2個あまった
りんごをつめ終わったあとの話です。
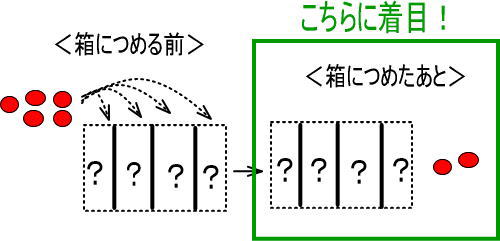
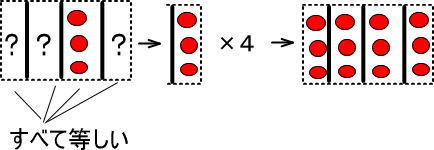
4つの箱のうち、1つの箱に着目したのが「商」でした。
いま、商は3なので、1つの箱には3個のりんごがはいっていますね。
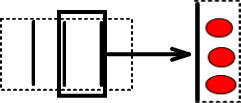
4つの箱は、すべて等しいのでした。
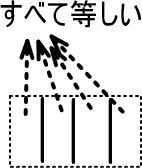
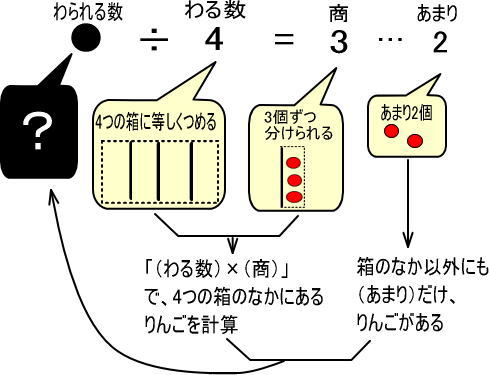
つまり、「3個ずつはいっている箱」を4つコピーすれば、すなわち「×4」すれば、4つの箱の中にいくつりんごが入っているのかわかります。
よって、箱のなかには「3×4=12」のりんごがあるとわかります。
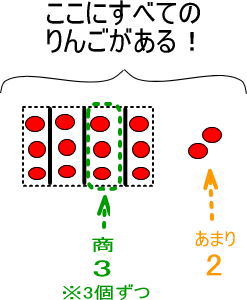
さて、あまりがないように、すべてのりんご、すなわち●個のりんごを4つの箱につめました。すると、りんごが2個あまりました。
つまり、4つの箱のすべてのりんごとあまったりんごを足し合わせば、●がいくつなのかわかります。
よって、つぎのようになります。
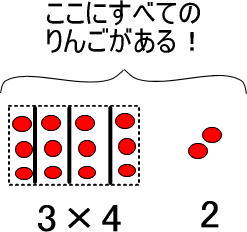
というわけで、●は「3×4+2=14」となります。
さて、ここで元の式をもう一度見てみてください。
それぞれのイメージです。
りんご●個を4つの箱につめ終わったあとの話です。
4つの箱にはいっているりんごと、あまりのりんごを足しあわせれば、すべてのりんごの数が計算できました。
よって、「(わられる数)=(わる数)×(商)+(あまり)」という式がでてくるわけですね。
スポンサード リンク
高校受験の文章題で出題!
「(わられる数)=(わる数)×(商)+(あまり)」という式は、高校受験の文章題で使うことがあります。
「わられる数」「わる数」「商」「あまり」とはどういうものなのかしっかりイメージできていると式が思いつくので、いまのうちからイメージできるようにしておきましょう。