あまりの性質を理解しよう!
※先に、「箱」をイメージすれば「(わられる数)=(わる数)×(商)」の式がわかる!から読んでください。
「6÷3=2」は、つぎのように考えるのでした。
・6 → りんごが6個あった
・÷3 → 3つの箱に等しくつめていった
・2 → 箱にはりんごを2個ずつつめることができた
これを図にすると、つぎのようになります。
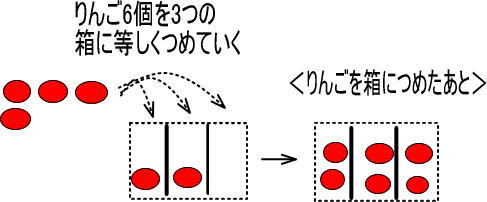
さて、ここでりんごの数を6個から、1個増やしたとします。
つまり、「6+1=7」の7個のりんごを3個の箱につめていったとします。
どうなると思いますか。
つぎのようになりますよね。
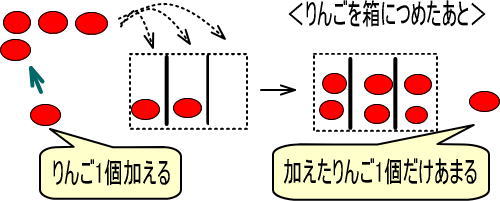
よって、つぎのようになります。
・りんご6個あって、そこにりんご1個加えた → 「6+1=7」
・3つの箱に等しくつめていった → ÷3
・箱には2個ずつはいっている → 2
・りんごが1個あまっている → ・・・1
式で表すと「7÷3=2・・・1」となります。
さて、ここでりんごの数を6個から、2個増やしたとします。
つまり、「6+2=8」の8個のりんごを3個の箱につめていったとします。
どうなると思いますか。
つぎのようになりますよね。
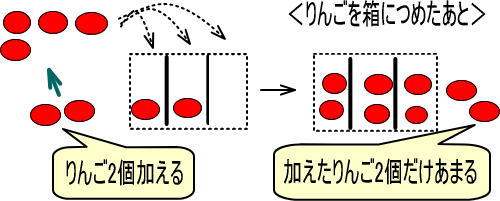
よって、つぎのようになります。
・りんご6個あって、そこにりんご2個加えた → 「6+2=8」
・3つの箱に等しくつめていった → ÷3
・箱には2個ずつはいっている → 2
・りんごが2個あまっている → ・・・2
式で表すと「8÷3=2・・・2」となります。
さて、ここでりんごの数を6個から、3個増やしたとします。
つまり、「6+3=3」の9個のりんごを3個の箱につめていったとします。
どうなると思いますか。
つぎのようになると思いますか?
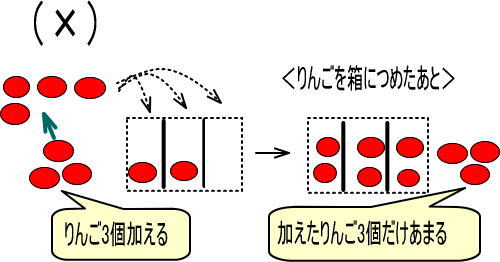
ちがいますよね。
なぜ間違いだと思いますか。
そうですね。
3個のりんごは、3つに箱に等しく分けられるためです。
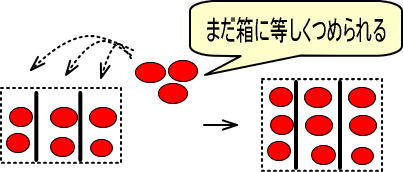
よって、つぎのようになります。
・りんご6個あって、そこにりんご3個加えた → 「6+3=9」
・3つの箱に等しくつめていった → ÷3
・箱には3個ずつはいっている → 3
・あまりはない
式で表すと、「9÷3=3」となります。
さて、りんごが6個あって、そこにりんごを4個加えたとします。
これを等しく3つに分けると、どうなると思いますか。
つぎのようになると思いますか。
ちがいますよね。
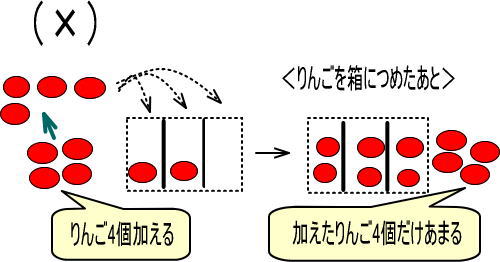
4個のりんごのうち、3個は等しく分けることができます(4個のうち、1個はあまります)。
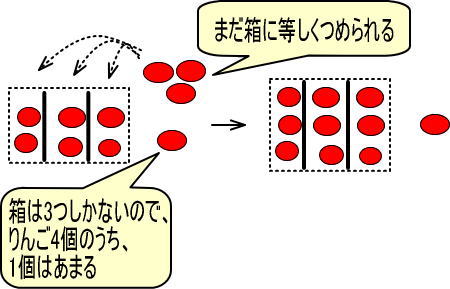
よって、つぎのようになります。
・りんご6個あって、そこにりんご4個加えた → 「6+4=10」
・3つの箱に等しくつめていった → ÷3
・箱には3個ずつはいっている → 3
・りんごが1個あまっている → ・・・1
式で表すと「10÷3=3・・・1」となります。
りんごが6個あって、そこにりんごを5個加えたとします。
これを等しく3つに分けると、どうなると思いますか。
つぎのようになると思いますか。
ちがいますよね。
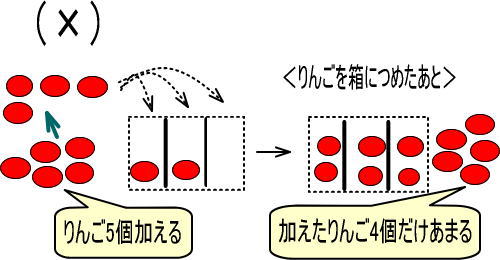
5個のりんごのうち、3個はつぎのように等しく分けることができます。
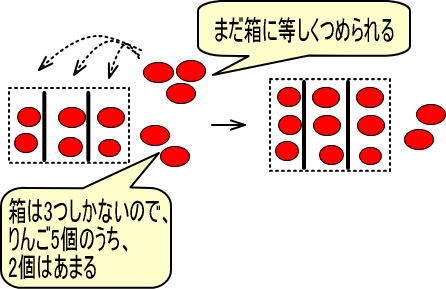
これを式で表すと、つぎのようになります。
・りんご6個あって、そこにりんご5個加えた → 「6+5=11」
・3つの箱に等しくつめていった → ÷3
・箱には3個ずつはいっている → 3
・りんごが2個あまっている → ・・・2
式で表すと「11÷3=3・・・2」となります。
スポンサード リンク
あまりは「÷●」の「●」を超えることはない!
以上の図を並べてみます。
何か気がつきませんか?
ヒントは「あまり」です。
<6個のりんごを、3つの箱に等しくつめていった場合>
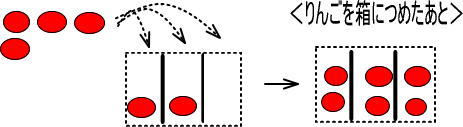
<6個のりんごに、りんごを1個加えてから、3つの箱に等しくつめていった場合>
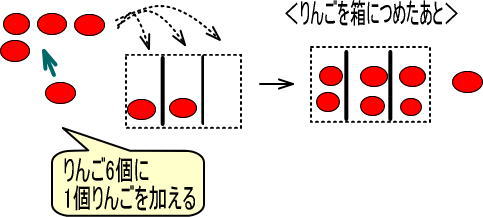
<6個のりんごに、りんごを2個加えてから、3つの箱に等しくつめていった場合>
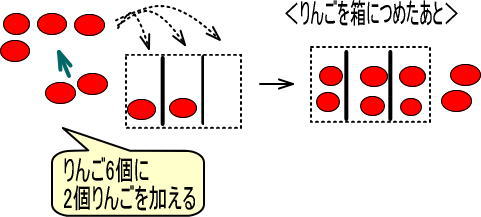
<6個のりんごに、りんごを3個加えてから、3つの箱に等しくつめていった場合>
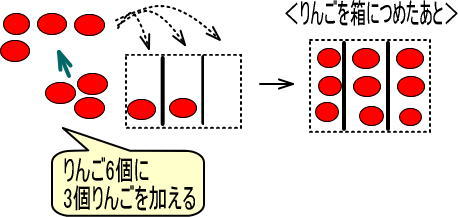
<6個のりんごに、りんごを4個加えてから、3つの箱に等しくつめていった場合>
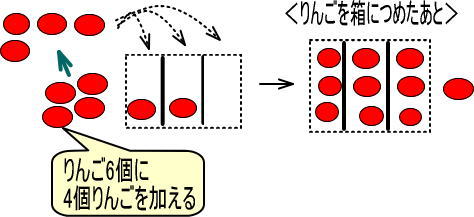
<6個のりんごに、りんごを5個加えてから、3つの箱に等しくつめていった場合>
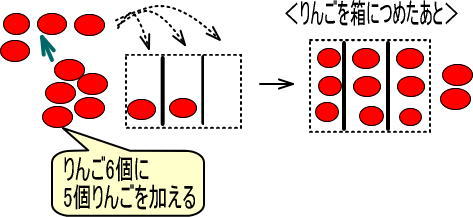
加えたりんごの数は「1」「2」「3」「4」「5」と増えているのに、あまりは「1」「2」「0」「1」「2」と、「3」を超えません。
なぜだと思いますか(じっくり上図を見れば気がつくと思います)。
そうですね。
加えたりんごの数が3個になれば、3つの箱にいれることができるためです。
・りんご1個加えた → あまり1
・りんご2個加えた → あまり2
・りんご3個加えた → りんごが3個になったので、3つの箱に等しくつめることができる → あまりなし
・りんご4個加えた → りんごが3個あるので3個分のりんごは3つの箱に等しくつめることができる。りんご1個あまっている → あまり1
・りんご5個加えた → りんごが3個あるので3個分のりんごは3つの箱に等しくつめることができる。りんご2個あまっている → あまり2
これを式で見てみましょう。
先ほどの式をまとめてみます。
6÷3=2
7÷3=2・・・1
8÷3=2・・・2
9÷3=3
10÷3=3・・・1
11÷3=3・・・2
じっくりとみると、あまりは「÷3」の「3」を超えることがないことに気がつくと思います。
※「÷3」は「箱が3つある」という意味のため、りんごが「3個」になるたびに箱に分けられます。
ほかに例をあげてみます。
「●÷2」の「÷2」は「2つ箱がある」という意味なので、「あまり2」「あまり3」のようにはなりません。
かならず、「あまりなし(すべてのりんごを2つの箱に等しくつめられる)」「あまり1」のいずれかになります。
※信じられないのなら、たとえば「6÷2」「7÷2」「8÷2」「9÷2」などと計算してみてください。あまりがないか、あまり1のいずれかになります。
このように、あまりは「÷●」の「●」を超えることはないという性質があります。
スポンサード リンク
筆算であまりを出す
これからわり算の計算をする機会がありますが、たいてい図にするのは難しいので、「筆算」を使って計算します。
たとえば「51÷5」を計算する場合、「51個のりんごを5つに等しく分ける」をすぐにイメージできないので、つぎのように筆算を使って計算します。
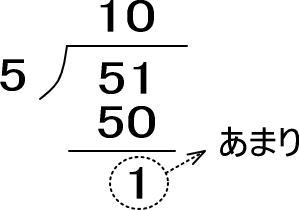
あまりは1です。
よって、「51÷5=10・・・1」となります。
このように筆算を使えば、りんごの図を描かなくても計算できてしまいますが、「あまり」がどういうものなのかしっかりイメージできないと別のところでつまづくことがあります。
りんごの図で、あまりとはどういうものなのか、しっかり理解しておきましょう。