速さ、道のり、時間に関する3つの式
「12÷4=3」です。
この式は「『12』を『3』にするには、『4』で割ればいい」という意味にもなりますね。
図で表すと、つぎのようになります。
<「12」を「3」にする>
![]()
<そのためには「4」で割る>
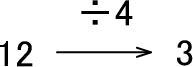
上図の→をぐにゃりと曲げてみました。
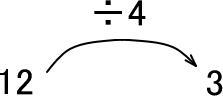
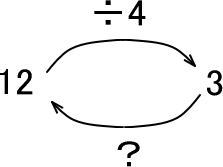
さて、「3」を「12」にするには、どうすればいいと思いますか。
4をかければいいですね。
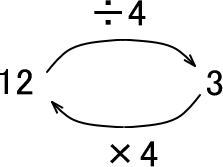
というわけで、「÷」の逆は「×」です。
この図、どこかで見た覚えはないですか?
そうですね。
かけ算とわり算の不思議な関係で学習したものとほとんど同じですね。
本題です。
(道のり)÷(時間)=(速さ)でした。
※(速さ)=(道のり)÷(時間)としても、(道のり)÷(時間)=(速さ)としても同じです。
この式は「『道のり』を『速さ』にするには『時間』で割ればいい」という意味にもなりますね。
<「道のり」を「速さ」にする>
![]()
<そのためには「時間」で割る>

上図の→をぐにゃりと曲げてみました。
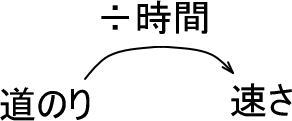
さて、「速さ」を「道のり」にするには、どうすればいいと思いますか。
「÷」の逆は「×」でしたね。
よって、つぎのようになります。
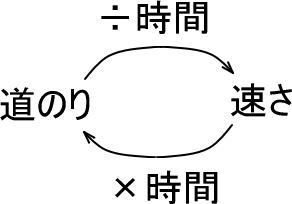
よって、(速さ)×(時間)=(道のり)になります。
話をまとめます。
つぎの式を勉強しました。
・(速さ)=(道のり)÷(時間)
この式の形を変えると、つぎの式になりました。
・(道のり)=(速さ)×(時間)
ここでは詳細は書きませんが、式の形を変えると、つぎの式がでてきます。
・(時間)=(道のり)÷(速さ)
これらの3つの式を覚えてほしいのですが…。
覚えられないですよね。
そこで、「きはじの図」の登場です。
スポンサード リンク
まずは「きはじの図」を描けるようになろう!
1.まずは、紙に下図を描きます。
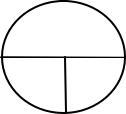
2.空欄に「き」「は」「じ」を書きこみます。国語では文章を「上から下」、「左から右」に読みますが、それと同じく「き」「は」「じ」も「上から下」「左から右」の順に埋めていきます。
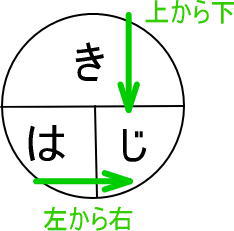
3.この図に「÷」「×」を書きこみます。どこに書きこめばいいのでしょうか。
つぎのように考えます。
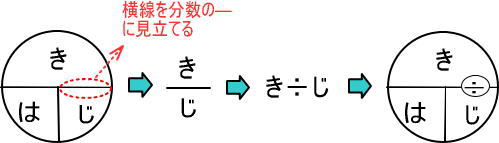
同じように、つぎのように考えます。
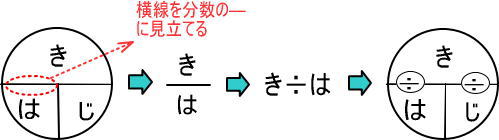
またつぎのように考えます。
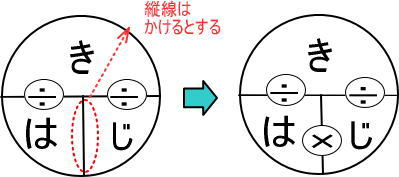
これで完成です!
さて、この「き」「は」「じ」はどういう意味でしょうか。
・き → 距離の「き」(距離は道のりと同じです)
・は → 速さの「は」
・じ → 時間の「じ」
というわけで、速さの文章題のときに、この「きはじの図」を書くようにしましょう。
では、どのように使えばいいのでしょうか。
スポンサード リンク
つぎは「きはじの図」の使いかたを覚えよう!
時速4kmで3時間歩くと、何km進めるのかを求めてみましょう。
1.まずは、問題文にある数値を、きはじの図にあてはめます。
問題文には、つぎの数値があります。
・速さ:時速4km
・時間:3時間
この2つの数値を、きはじの図に書きこみます。
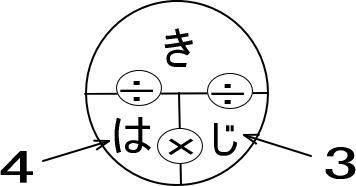
2.速度の文章題では「速さ」「距離(道のり)」「時間」のいずれかを求めますが、求めるものを手で隠します。
問題文には「何km進めるのか」とあります。
距離を求めるわけなので、距離の「き」を手で隠します。
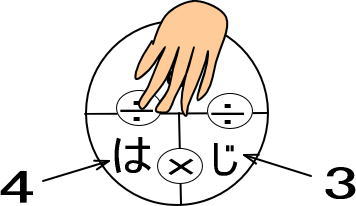
3.式がでてくるので計算します。
「は×じ」、すなわち「4×3」という式がありますよね。
よって、答えは12kmとなります。
スポンサード リンク
実際に「きはじの図」を使ってみよう!
A町からB町まで9kmあります。
太郎君はA町からB町まで時速3kmで歩きました。何時間後にB町に着きますか。
このような速さに関する問題は、まずは「地図」を描けばいいのでした。
場所は「A駅」「B駅」で、道のりは9kmです。
登場人物は太郎君で時速3kmです。
あとは「時間」を書きこめばいいのですが、時間はのっていないので書きこみません。
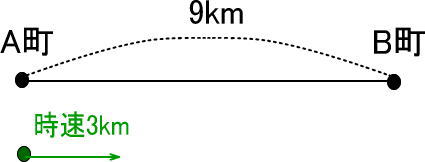
さて、いま、太郎君はA町からB町まで何時間で歩いたのか、要は「時間」を求めたいのですね。
ここまでのことがわかれば、きはじの図を使います。
1.まずは、問題文にある数値を、きはじの図にあてはめます。
問題文には、つぎの数値があります。
・距離:9km
・速さ:時速3km
この2つの数値を、きはじの図に書きこみます。
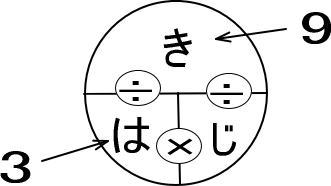
2.速度の文章題では「速さ」「距離(道のり)」「時間」のいずれかを求めますが、求めるものを手で隠します。
時間を求めるわけなので、時間の「じ」を手で隠します。
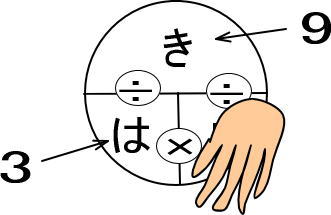
3.式がでてくるので計算します。
「き÷は」、すなわち「9÷3」の式がありますね。
よって、3時間となります。
ちなみに、「地図を描かなくても、いきなり、きはじの図を使えばいいのではないか」と思ったひともいるかもしれません。
しかし、もっと複雑な問題を解くときに、地図を描けないと解くことができませんので、「今後のための練習」で地図を書きましょう。
いつの日か「きはじの図」からは卒業しよう!
「きはじの図」は便利です。
だからといって、速さとは何なのか理解していないと、将来、つまづきます。
いつの日か、きはじの図から卒業できるようになってくださいね!
あくまで「算数を勉強しているひと」「数学が苦手なひと」に向けた解きかたですから。
※参考までに、数学が得意になると、速度は「単位時間あたりの距離」などと考えます。